Valódi véletlen változó

A valódi véletlen változó olyan véletlen változó, amelynek értéke vagy annak része van  ; ez egy véletlenszerű kísérlet lehetséges eredményeinek halmazából meghatározott függvény , amelynek képesnek kell lennünk meghatározni annak valószínűségét, hogy egy adott értéket vagy egy adott értékkészletet vesz fel. A valódi véletlen változók a leggyakrabban vizsgált véletlen változók, ami arra készteti néhány szerzőt, hogy hagyja ki a valós jelzőt , és röviden véletlen változóról beszéljen. R{\ displaystyle \ scriptstyle \ mathbb {R}}R{\ displaystyle \ scriptstyle \ mathbb {R}}

A véletlen változókat széles körben használják a valószínűségelméletben és a statisztikákban . Az alkalmazásokban véletlen változókat használnak egy nem determinisztikus mechanizmus eredményének modellezésére, vagy egy nem determinisztikus kísérlet eredményeként, amely véletlenszerű eredményt generál. A matematikai vagy következtetési statisztikákban véletlen változókat szoktak használni a végtelennek vélt populációk modellezésére.

Ez a cikk csak a valós véletlenszerű változókkal foglalkozik  :

• A cikk véletlen változó általánosítja ezt a cikket a nem valós esetben a szempontból az elmélet mérés  ;
• Az Elemi véletlen változók című cikk intuitívabban közelíti meg a véletlen változó fogalmát .

Részletek

• Eredetileg egy változó nyerési függvény volt, amely a játék kimenetele eredményeként kapott nyereményeket képviselte Tegyük fel például, hogy egy játékos dob egy kockát, és az a játékos nyer 1 eurót, ha hatot dob, és 10 eurót veszít, ha újabb eredményt dob. Ezután meg lehet határozni azt a véletlenszerű változót, amely 1-et a "hat" eredménnyel és a -10-et érdektelen eredménnyel társít. Annak a valószínűsége, hogy a véletlen változó eléri az 1 értéket, pontosan megfelel annak a valószínűségnek, hogy a játékos nyer 1 € -t .

• A legegyszerűbb valódi véletlen változót a dobás vagy halom játékának eredménye adja, amely elem vagy arc . Egy másik egyszerű példát egy kockadobás eredménye ad, amelynek lehetséges értékei 1, 2, 3, 4, 5 vagy 6 (ha a kocka klasszikusan köbös). Az ilyen valós véletlen változókat diszkrétnek minősítik, mert jól elkülönített értékeket vesznek fel. Ezzel szemben a populációból véletlenszerűen vett egyed nagyságának mérése inkább egy valós pozitív számra hasonlít (ez sem teljesen igaz, mert az ergonómiai kérdések annál valószínűtlenebbé teszik. Jelentős tizedesjegyű szám kijelentése; az attraktor valójában fraktál ). Ezt a valós véletlen változót azután konvenció szerint folytonosnak minősítik . A véletlen változó által vett értékek eloszlásának tanulmányozása a valószínűség törvényének fogalmához vezet .

• A matematika, és pontosabban valószínűségszámítás , a véletlen változó egy mérhető függvény definiált egy valószínűségi mezőn . A megfelelő képméretet a véletlen változó törvényének nevezzük . Ez a fajta függvény egy véletlenszerű jelenség modellezésére szolgál , például egy kockadobás eredményére. A Lebesgue-integrál érdekes tulajdonsága, hogy a szigorúan nulla valószínűségű esemény nem feltétlenül lehetetlen a kifejezés szoros értelmében (tehát vegyük figyelembe a [0, 1] intervallumban véletlenszerűen rajzolt valós értéket ; annak valószínűségét, hogy a racionális nulla, míg az racionálisok ebben az intervallumban végtelen halmazt alkotnak, sőt mindenhol sűrűek ).

Néhány valós véletlen változó

A valós véletlenszerű változók definícióinak bevezetéseként érdekesnek tűnik egy széles körben használt változók családjának rövid bemutatása.

Azon bizonyos változó mellett, amely egy adott értéket 1-es valószínűséggel vesz fel, a legegyszerűbb valós véletlen változót Bernoulli változójának nevezzük . Ehhez két állapotra van szükség, amelyeket mindig lehet kódolni 1 és 0, p és 1- p valószínűséggel . Egyszerű értelmezés egy kockajátékra vonatkozik, amelyben az ember egy eurót nyerhet a hat húzásával ( p = 1/6). Játékok sorozatánál a győzelmek átlaga általában p, mivel a játékok száma a végtelenségig hajlik.

Ha figyelembe vesszük, hogy egy részt csak egy rajz helyett n húzás alkot , akkor a nyereségek összege egy binomiális változó megvalósulása, amely az egész egész értéket 0-tól n- ig veheti fel . Ennek a változónak az átlaga a termék np . Kevésbé triviális példát kapunk, ha figyelembe vesszük egy jelölt pontszámát egy választási szavazáson .

Ha n elég nagy és p nem túl kicsi, megfelelő közelítést találhatunk a Gauss változó segítségével . Felmérésekben ez lehetővé teszi a megbízhatósági intervallum társítását a nyers eredménnyel. Így 100-ból 95 esély van arra, hogy egy 1000 fős felmérés helyes eredményt adjon ± 3% -on belül.

Még mindig nagy n esetén a Poisson- közelítés előnyösebb, ha p elég kicsi ahhoz, hogy az átlagos np ne legyen túl nagy, néhány egység nagyságrendű. Egy felmérésben ez lenne a „kis” jelöltekre alkalmazandó jog. Főként a sorban állási problémákra alkalmazott törvény.

Az összeg négyzetének ν független Gauss változók egy változót χ 2 és ν szabadsági fok (az exponenciális változó egy speciális esete ennek). A χ 2 tesztet a valószínűségi törvény megfelelőségének értékének értékelésére használják egy empirikus eloszláson.

Ha egy Gauss-változót elosztunk egy variable (az előző négyzetgyöke) változóval , akkor egy Student változót kapunk . Két független χ 2 változó aránya meghatározza a Snedecor változót . Ezt a két törvényt alkalmazzák az állítólagosan Gauss-populációk elemzésében.

Alapok

A valószínűség törvénye

• Egy valós véletlen változó törvénye részletesen leírja ennek a változónak az értékeit. Az X változó törvénye tartalmazza az összes eloszlási függvény kiszámításához szükséges információt, várakozását és általánosabban pillanatait, jellegzetes függvényét, mediánját és kvantileit.
• Más szóval, ha két igazi valószínűségi változók X és Y azonos törvénye valószínűség, akkor ugyanolyan eloszlás, ugyanaz a várakozás és még általánosabban az azonos pillanatokban, ugyanaz a karakterisztikus függvény, ugyanaz a medián és az azonos kvantilisek.
• Annak a valószínűsége törvény valódi véletlen változó X jelentése az adatokat az értékek igen nagy csoportját alkatrészek A az a Borelian törzs , ideértve különösen az időközönként. Például, a törvény X értékét adja meg , bármely választott a valós számok egy < b , ami megfelel a kiszámítása a választott A = [ a , b ] , vagy az értéke , bármely választás a valós x szám , amely megfelel az A =] –∞, x ] választás számításának .P(x∈NÁL NÉL){\ displaystyle \ mathbb {P} (X \ A-ban)}R{\ displaystyle \ mathbb {R}}P(nál nél≤x≤b){\ displaystyle \ mathbb {P} (a \ leq X \ leq b)}P(x∈NÁL NÉL){\ displaystyle \ mathbb {P} (X \ A-ban)}P(x≤x){\ displaystyle \ mathbb {P} (X \ leq x)}P(x∈NÁL NÉL){\ displaystyle \ mathbb {P} (X \ A-ban)}
• Szerint a matematikai definíciója (lásd cikkünket a véletlen változó részleteket), a törvény X a mérés valószínűsége meghatározott bármely elem egy a Borel a kapcsolatotPx{\ displaystyle \ mathbb {P} _ {X}}R{\ displaystyle \ mathbb {R}}

Px(NÁL NÉL)=P(x∈NÁL NÉL)=P(x-1(NÁL NÉL)).{\ displaystyle \ mathbb {P} _ {X} (A) = \ mathbb {P} (X \ -ban A) = \ mathbb {P} \ balra (X ^ {- 1} (A) \ jobbra).}

• A valódi véletlenszerű változó törvénye lehet diszkrét vagy sűrűségű (a Lebesgue- on mérve ). Ez a két leggyakoribb eset az alkalmazásokban.R{\ displaystyle \ mathbb {R}}

Elosztási funkció

Ezt a fogalmat bármelyik korábban figyelembe vett változóból be lehetne vezetni, de egyértelműbbnek tűnik a szerszám esetének más szögből történő vizsgálata. Valójában meghatározza az X véletlenszerű változót, amely ugyanolyan valószínűségű (1/6) értékeket vesz fel az {1,2,3,4,5,6} halmazban. Tudjuk majd társítani semmilyen valós értéke x a valószínűsége, hogy egy döntetlen kisebb vagy egyenlő, mint x , amely meghatározza a lépcsős görbe, melynek lépései magassága megegyezik a 1/6.

Formálisan ez elosztási függvényhez vezet

Fx(x)=P(x≤x){\ displaystyle F_ {X} (x) = \ mathbb {P} (X \ leq x) \,}

Ebben az X nagybetű a valós véletlenszerű változót, a numerikus értékek halmazát, az x kisbetű pedig a állapot szokásos értelmében változó állapotváltozót jelöli.

Ha az események már nem egyenletesek, ez csak torzítja a görbét. Egy új koncepció bevezetése érdekében kezdhetjük úgy, hogy a szerszámot hatszámú rulettre cseréljük (ami szigorúan azonos problémához vezet). Ezután nem változtatunk semmi alapvetően, ha a hat egész számot 60 fokos ívközéppontok referenciajeleivel helyettesítjük. Innentől kezdve a szektorok számának növelésével csökkenthető a méretük: a fokok egyre kisebbek lesznek, amíg megkülönböztethetetlenek egy rajzon. A határig való áthaladás a diszkrét változót folytonos változóval helyettesíti, amely az összes valós értéket a] 0,360] intervallumban veszi fel: ez egy egységes változó.

Az eloszlásfüggvény (tág értelemben) növekszik a ] –∞, + ∞ [ intervallumban , és bármely ponton jobbra halad; –0 felé halad –∞ és 1 felé + ∞ . Ezzel szemben bármely funkció, amely kielégíti az előző tulajdonságokat (jellemzőket), véletlen változó eloszlásfüggvényének tekinthető.

Az eloszlásfüggvény érdeke abban rejlik, hogy jól definiálható mind a folytonos halmazon definiált folyamatos változók, mind pedig a megszámlálható halmazon definiált diszkrét változók esetében (a legtöbb gyakorlati esetben ez egyenlő távolságra halmazra redukálódik, amelyek egész számhalmazra redukálható). Egy olyan elosztási függvény progresszív cseréje (közelítése), amelynek görbéjét egy folyamatos eloszlású függvény lépteti, lehetővé teszi, hogy intuitív módon lássuk, hogyan képes egy folyamatos változó olyan közelítést adni, amelyet gyakran könnyebb kezelni, mint a változó. A diszkrét változók folyamatos változókkal történő ilyen közelítésének matematikai megfogalmazását lásd a Konvergencia a törvényben című cikkben .

Folyamatos változó valószínűségi sűrűsége

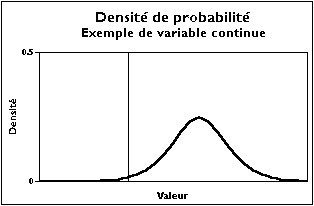
A folytonos változónak gyakran van egy eloszlásfüggvénye, amely minden ponton folytonos és darabonként megkülönböztethető. Ezután kényelmes levezetni a valószínűségi sűrűség megszerzéséhez, ellenőrizve:

ox(x)=dFxdx(x){\ displaystyle p_ {X} (x) = {\ frac {{\ \ textrm {d}} F_ {X}} {{\ textrm {d}} x}} (x)}

amely definiálva van, és pozitív (vagy nulla) értékekkel rendelkezik a ] –∞, + ∞ [ értéken , olyan, hogy . ∫-∞+∞ox(x) dx=1{\ displaystyle \ int _ {- \ infty} ^ {+ \ infty} p_ {X} (x) \ {\ textrm {d}} x = 1}

Az eloszlásfüggvényt a relációval rekonstruáljuk:

Fx(x)=∫-∞xox(ξ) dξ{\ displaystyle F_ {X} (x) = \ int _ {- \ infty} ^ {x} p_ {X} (\ xi) \ {\ textrm {d}} \ xi}

Általános okokból gyakran kényelmes ezeket a képleteket differenciális formában megírni:

P(x<x≤x+dx)=ox(x) dx{\ displaystyle \ mathbb {P} (x <X \ leq x + {\ textrm {d}} x) = p_ {X} (x) \ {\ textrm {d}} x}

Ha az Y = f ( X ) képlet alapján változóváltást hajtunk végre , akkor az új valószínűségi sűrűséget a következő képlettel számoljuk ki:

oY(y)dy=ox(x)dx{\ displaystyle p_ {Y} (y) {\ textrm {d}} y = p_ {X} (x) {\ textrm {d}} x \,}

Diszkrét változó valószínűségi függvénye és valószínűségi sűrűsége

Az X diszkrét véletlen változó törvényét az értéke valószínűségi halmaza határozza meg, amelyet valószínűségi függvénynek hívunk ( angolul tömegfüggvény ). Ha feltételezzük, hogy egész számokat vesz fel (bármely előjelből), akkor ezt írjuk:

∀k∈Z,ox(k)=P(x=k){\ displaystyle \ forall k \ in \ mathbb {Z}, p_ {X} (k) = \ mathbb {P} (X = k)}

Az X diszkrét véletlen változó implikálásával az alábbiak szerint egyszerűsíthetjük a jelölést:

∀k∈Z,ok=P(x=k){\ displaystyle \ forall k \ in \ mathbb {Z}, p_ {k} = \ mathbb {P} (X = k)}

Az eloszlásfüggvényt (amelynek értékeit akkor kumulatív valószínűségnek nevezzük ) a relációval rekonstruáljuk :

∀nem∈Z,∀x∈[nem;nem+1[,Fx(x)=∑k=-∞nemok{\ displaystyle \ forall n \ in \ mathbb {Z}, \ forall x \ in [n; n + 1 [, F_ {X} (x) = \ összeg _ {k = - \ infty} ^ {n} p_ {k}}

Ha az eloszlásfüggvényt lépések vagy Heaviside függvények összegének tekintjük , akkor deriváltját impulzusok vagy Dirac függvények összegeként értelmezhetjük, ezért ezt írjuk:

∀x∈R,Fx′(x)=∑k∈Zokδk(x){\ displaystyle \ forall x \ in \ mathbb {R}, F '_ {X} (x) = \ sum _ {k \ in \ mathbb {Z}} p_ {k} \, \ delta _ {k} ( x)}

Ezután ellenőrizzük, hogy:

∀x∈R,ox(x)=Fx′(x){\ displaystyle \ forall x \ in \ mathbb {R}, p_ {X} (x) = F '_ {X} (x)}

Ez a „valószínűségi sűrűség” egy adott problémát érdekel: amikor az integrál valószínűségi sűrűséghez kapcsolódik, a Dirac függvény alapvető tulajdonsága lehetővé teszi az integrál egyszerű, a valószínűség függvényt tartalmazó összeggé történő átalakítását.

Elvárás

Definíciók

A valódi véletlenszerű változó matematikai várakozását e változó értékeinek "átlagaként" határozzuk meg, súlyozva az előfordulásuk valószínűségével. Folyamatos változó esetén a fent megadott differenciál képletet integrálják, az integrálhatóság függvényében

E[x]=∫-∞+∞x ox(x) dx.{\ displaystyle \ mathbb {E} [X] = \ int _ {- \ infty} ^ {+ \ infty} x \ p_ {X} (x) \ {\ textrm {d}} x.}

Ez az összeg jobban ismert, mint átlag.

X , hogy egy igazi véletlen változót, függvényt f állítólagos rendszeres definiál egy új valószínűségi változó f ∘ X jegyezni f ( X ) amelynek várakozás, ha az létezik, van írva helyettesítjük x által f ( x ) az előző általános képletű ( transzfer tétel ) .

E[f(x)]=∫-∞+∞f(x) ox(x) dx.{\ displaystyle \ mathbb {E} [f (X)] = \ int _ {- \ infty} ^ {+ \ infty} f (x) \ p_ {X} (x) \ {\ textrm {d}} x .}

Diszkrét változó esetén a „valószínűségi sűrűség” az összegezhetőség függvényében ahhoz vezet

E[f(x)]=∑k=-∞+∞f(k) Px(k).{\ displaystyle \ mathbb {E} [f (X)] = \ összeg _ {k = - \ infty} ^ {+ \ infty} f (k) \ P_ {X} (k).} Jellemző funkció

Ha az X tényleges véletlen változó valószínűségi sűrűségfüggvényének van egy Fourier-transzformációja , akkor ezR{\ displaystyle \ mathbb {R}}

ϕx(t)=E[eéntx]{\ displaystyle \ phi _ {X} (t) = \ mathbb {E} [{\ textrm {e}} ^ {itX}] \,}

változó jellegzetes függvényének nevezzük .

Pillanatgeneráló funkció

A funkció generáló a pillanatok egy valószínűségi változó X határozza

Mx(t)=E(etx),t∈R,{\ displaystyle M_ {X} (t) = \ mathbb {E} \ left ({\ textrm {e}} ^ {tX} \ right), \ quad t \ in \ mathbb {R},}

amikor reménye létezik. Ezt a függvényt, amint a neve is sugallja, az X véletlen változó valószínűségi eloszlásához kapcsolódó idők előállítására használják . Ez lehetővé teszi egy törvény additivitásának meghatározását is.

Pillanatok

Ha egy véletlen változó jellegzetes függvényét (vagy generáló függvényét) sorba lehet fejleszteni, akkor ez feltárja ennek a momentumait , a k sorrend momentuma pedig

mk≡E[xk]{\ displaystyle m_ {k} \ equiv \ mathbb {E} [X ^ {k}] \,}.

Egy meglehetősen szabályos változó gyakorlatilag fontos esetben ezért jellemezhető a momentumainak sorrendjével, jellemző funkciójával vagy generáló funkciójával, valószínűségi sűrűségével vagy esetleg valószínűségi függvényével vagy eloszlásfüggvényével.

Általános esetben csak az első pillanatok létezhetnek.

Gyakorlati eszközök

Pillanatok és pillanatok középre

Az első sorrend pillanata , a változó várakozása vagy átlaga ,

μ≡m1=E[x],{\ displaystyle \ mu \ equiv m_ {1} = \ mathbb {E} [X], \,}

egy mutatója központi tendenciát .

A magasabb rendű pillanatok kiküszöbölik ezt a helyzetparamétert, figyelembe véve a középre változót, kivonva annak átlagából.

A második rend központi mozzanata,

σ2≡m2′=E[(x-μ)2],{\ displaystyle \ sigma ^ {2} \ equiv m '_ {2} = \ mathbb {E} \ bal [\ bal (X- \ mu \ jobb) ^ {2} \ jobb], \,}

egy indikátora diszperzió úgynevezett variancia . Az σ négyzetgyököt , az alapmennyiséggel homogén mennyiséget szórásnak nevezzük . Ha a véletlen változó egy véletlenszerű folyamat adott időpontjában érvényes érték, akkor általában a közép-négyzet alapértelmezett kifejezést részesítjük előnyben.

Ez a két mozzanat a változóval kapcsolatos információk fontos részét adja, mindezt, ha normálisnak tekinthető .

A magasabb rendű momentumok, amelyek a többi változó esetében további részleteket adnak az eloszlás alakjáról, a redukált középre változóhoz kapcsolódnak, amelyet méretnélkülivé tesznek a standard szórásával osztva.

A csökkentett középpontú változó harmadrendű momentuma,

m3′=E[(x-μσ)3],{\ displaystyle m '_ {3} = \ mathbb {E} \ left [\ left ({\ frac {X- \ mu} {\ sigma}} \ right) ^ {3} \ right], \,}

az aszimmetria mutatója .

A csökkentett központú változó negyedik rendű momentuma,

m4′=E[(x-μσ)4],{\ displaystyle m '_ {4} = \ mathbb {E} \ left [\ left ({\ frac {X- \ mu} {\ sigma}} \ right) ^ {4} \ right], \,}

a kurtosisnak nevezett eloszlások szélsőségeinek laposodása .

Medián és kvantilis

X véletlenszerű változó mediánját hívjuk , valódi m-et olyannak, hogy

P(x≤m)≥1/2≤P(x≥m){\ displaystyle \ mathbb {P} (X \ leq m) \ geq 1/2 \ leq \ mathbb {P} (X \ geq m)}

Diszkrét véletlenszerű változó esetén ez a meghatározás nem túl érdekes, mert több medián létezését teszi lehetővé

ha X a tökéletesen kiegyensúlyozott 6 oldalú szerszám felső oldalán megjelenő szám, bármely valós m esetén szigorúan 3 és 4 között van: P(x≤m)=P(x≥m)=1/2{\ displaystyle \ mathbb {P} (X \ leq m) = \ mathbb {P} (X \ geq m) = 1/2}

vagy olyan medián létezése, amely nem ad 0,5 valószínűséget.

Ha X az az összeg, amelyet két tökéletesen kiegyensúlyozott, 6 oldalas kocka dobásával kapunk. X- nek csak egy mediánja van 7, deP(x≤7)=21/36{\ displaystyle \ mathbb {P} (X \ leq 7) = 21/36}

Folyamatos változó esetén , ha az eloszlásfüggvény szigorúan növekszik, a definíció megegyezik a következőkkel:

az X mediánja az egyedi valós m, így F X ( m ) = 0 {,} 5 .

Az a tény, hogy az eloszlásfüggvény folyamatos és feltételezhetően szigorúan növekszik, értéke 0 0; 1 [ , biztosítja a medián létét és egyediségét.

Ha a medián értéke m = 0,5 , akkor lehet érdeklődni más m értékek iránt is (amelyeket kvantilisoknak nevezünk ):

• Kvartilis: m = 0,25, 0,75
• Decil: m = 0,1, 0,2, 0,3 ...
• Százalék: m = 0,01, 0,02 ...

Véletlen változó szimulációja

Az véletlen szimulálására gyakran ál-véletlen generátorokat használnak . A fizikai jelenségek meghatározhatatlanságának kiaknázására is van mód, például egy lávalámpa- film variációinak elemzésével, a termikus zaj elemzésével , vagy még jobb, ha a kvantum természetét kérjük meg dobni a kockát.

Lásd is

• Véletlen változók konvergenciája
• Többváltozós valószínűségi törvény
• Ál-véletlenszám-generátor
• Véletlenszám-generátor
• A valószínűség törvénye
• Elemi véletlen változók