Síkgrafikon
A gráfelméletben a síkgráf olyan gráf, amelynek sajátossága, hogy képes ábrázolni önmagát egy síkon anélkül, hogy minden él (vagy ív egy irányított gráfnál) keresztezné a másikat. Más szavakkal, ezek a grafikonok pontosan azok, amelyeket be lehet vetni a síkba, vagy akár azok a grafikonok, amelyek kereszteződésének száma nulla.
Az ezekhez a grafikonokhoz kapcsolódó módszerek lehetővé teszik olyan problémák megoldását, mint a három ház rejtvénye, és olyan nehezebbeket, mint a négy szín tétele .
Példák és ellenpéldák
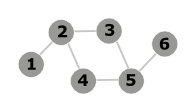
- Ez a gráf egyértelműen sík, mert két él között nincs metszéspont.
- Ez egy teljes gráf négy csúccsal (K 4 ). Sík: ha az 1 2 3 háromszögben mozgatjuk a 4 csúcsot , akkor azt látjuk, hogy nincs többé az élek metszéspontja.
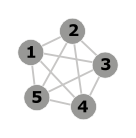
- Ez egy teljes gráf, 5 csúccsal (K 5 ). Nem sík.
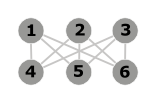
- Ez egy teljes kétoldalas gráf, amelynek 6 csúcsa van, ezek közül 3 kapcsolódik a másik háromhoz (K 3.3 ). Nem sík.
Valójában a K 5 és a K 3.3 a legkisebb nem sík gráf, ami az alábbi jellemzésből következik.
Kuratowski és Wagner jellemzése
A lengyel matematikus, Kazimierz Kuratowski 1930-ban hozta létre a síkgrafikonok következő jellemzését:
A véges gráf akkor és csak akkor síkbeli, ha nem tartalmaz részleges részgráfot, amely a K 5 (a teljes gráf 5 csúccsal) vagy a K 3.3 (a teljes kétoldalas gráf 3 + 3 csúccsal) kiterjesztése .A gráf kibővítése (vagy felosztása ) annak eredménye, hogy egy vagy több csúcsot hozzáadunk egy vagy több élhez (például az élt • —— • átalakítjuk • - • - • •).
Néhány évvel később Klaus Wagner német matematikus hasonló jellemzést adott:
A véges gráf akkor és csak akkor síkbeli, ha nem számolja K 5-et vagy K 3- at a kiskorúak között .A gráf kisebb része élek összehúzódásának (a végpontok egyesítésének), az élek eltávolításának (a végpontok összevonása nélkül) és a csúcsok (és a szomszédos élek) eltávolításának eredménye.
E két jellemzés között csekély a különbség, de Wagner feltételezései szerint ez utóbbi olyan általánosítást fog elismerni, amelyet Kuratowski nem. Úgy gondolta, hogy a kiskorúak által bezárt véges grafikonok minden egyes osztályához tartozik egy tiltott kiskorúak véges halmaza, amely ezt jellemzi. Azt mondják, hogy egy osztályt kiskorú zárja le, ha az az összes benne szereplő grafikon összes kiskorúját tartalmazza; például egy sík gráf mindig sík az élek és csúcsok összehúzódása vagy eltávolítása után, és ebben az osztályban a két tiltott kiskorú csak a K 5 és a K 3.3 . De különösképpen létezne véges számú tiltott kiskorú a grafikonok osztályában, amelyek elmerülhetnek egy tóruszon vagy bármilyen felületen, és azon gráfok osztályához, amelyek csomópont nélkül el tudnak merülni a háromdimenziós térben, többek között. Ezt a sejtést 2004-ben Robertson és Seymour végül bebizonyította, de nem konstruktív módon: például még mindig nem ismerjük az összes olyan kiskorúat, akinek tilalma van egy grafikon beillesztése a tóruszra. További információ a Robertson-Seymour tétel cikkében található .
Tulajdonságok
A bekezdés további részében a következő jelöléseket fogjuk használni:
- sík gráfot jelöl,
- a csomópontok száma,
- az élek (vagy linkek) száma,
- arcainak száma.
Az arc a gráf komplementerének összekapcsolt eleme a síkban. A mértéke egy arc a hossza a határ menti ciklus, úgy véljük, a lehető legrövidebb utat a származási tévesztendő össze a vége, az élek számát (azok multiplicitás) a mértéke az arc . Megjegyzik . Megkapjuk az első szinte nyilvánvaló képletet:
Valójában a ciklus minden éleleme két oldallal határolódik, a ciklus nélküli közös éleket kétszer keresztezi a gráf komplementerének határtalan összetevője.
Euler képlete és következményei
Az összekapcsolt sík gráf Euler-képlete :
Egyszerű módszer annak bizonyítására, ha létrehozunk egy ciklus nélküli gráfhoz (egy arccal), majd indukcióval adjuk hozzá azokat az éleket, amelyek ciklusokat generálnak. Ez a képlet megmutatja, hogy bármely összekapcsolt, legalább három csúcsú egyszerű síkbeli gráf kielégíti a következő növekedést.
Az egyszerű gráf egy olyan hurok nélküli grafikon (a hurok egy él, amelynek egybeeső kezdete és vége van) és több él nélkül (több él ugyanazon eredetű és azonos élű él). Ez a képlet egyszerűen bemutatható: bármelyik arc legalább 3-as fokozatú, mert a grafikonnak legalább három csomópontja van és egyszerű. Mi következtetni, az (1) képlet, hogy a 3 f kisebb, vagy egyenlő, mint 2 a . Euler képlete lehetővé teszi számunkra a következtetést.
Ez a képlet azt jelenti, hogy a sík gráfok üreges gráfok . Ezen kívül arboritásukat 3 határolja.
Ez a növekedés az eredete egy bizonyíték arra, hogy a K 5 nem planáris. Valóban, K 5 10 élek, és az 5 csomópont, ez az eredmény nem egyeztethető össze a növekedés (2). Ha a felső határ (2) feltételezéseivel a grafikon háromszög nélkül van , akkor megvan a felső határ:
Az érvelés megegyezik, de ezúttal egy arc mértéke legalább 4-vel egyenlő. Arra következtetünk, hogy a K 3,3 nem sík. A részletek a " Három ház talánya " című cikkben találhatók .
Euler képletének bemutatásaAz első lemma hasznos:
- Bármely összekapcsolt síkdiagram úgy kapható meg, hogy éleket csatol egy összekapcsolt fához, amelynek ugyanazok a csomópontjai vannak:
A fa olyan grafikon, amely csak egy arcot tartalmaz. Indukcióval haladunk f-n , a gráf arcainak számán.
Tegyük fel, hogy a grafikonnak csak egy arca van, a gráf egy fa, és a javaslat triviálisan igazolható. Tegyük fel, hogy az állítás igaz f , és jelenjen meg a gráf G a f + 1 arcok. A Jordan tétel azt mutatja, hogy ha több arc van, akkor van egy Jordan görbe , amelyet élek alkotnak. Ha levonjuk az egyik élek A görbéből a gráf G , a jobb és bal részei a komplement a grafikon, amely korábban kialakított két arca lett csak egy, és mi marad a Jordan-féle garantálja, hogy a G mindig csatlakozik . A amputálták grafikonja A megfelel az indukciós hipotézisek és kapjuk hozzáadásával élek egy csatlakoztatott fa. Hozzáadása az utolsó szélén A biztosítja a kezdeti gráf.
- Euler képlete:
Bizonyítsuk be először egy fa állítását, csomópontjainak n számával történő indukcióval . Ha a fa csak egyetlen csomópontot tartalmaz, akkor annak van arca és nincs éle, a képlet ellenőrzött. Feltételezzük, hogy a képlet igaz n-re , mutassuk meg egy n + 1 csomópontot tartalmazó G fára . Mivel a fa csak egyetlen arcot tartalmaz, legalább egy N csomópontot tartalmaz , amelyek egyetlen élhez kapcsolódnak (különben Jordan tétele garantálná legalább két arc létezését.). Az ettől a csomóponttól és a szomszédos éltől megfosztott G fa egy összekapcsolt fa, amely n csomópontot tartalmaz , kielégíti az indukciós hipotézist. Az N csomópont és a hozzá tartozó él hozzáadása egy csomópont és egy él hozzáadásának felel meg, Euler képlete továbbra is igaz marad G-re , amely befejezi ezt az első lépést.
Bizonyítsuk be most egy összekapcsolt gráfra vonatkozó tételt , az arca f számának indukciójával . Ha f egyenlő 1-vel, a képletet az előző megismétlődés szerint ellenőrizzük. Tegyük fel, hogy minden olyan gráfra igaz, amelynek f arca van, és mutassa meg azt a G gráfra, amelynek f + 1 arca van. A lemma megismétlődése azt mutatja, hogy lehet levonni egy élet G-ből úgy, hogy az új gráf továbbra is összekapcsolt legyen és pontosan f arccal rendelkezik. Euler képletét ezután indukciós hipotézissel ellenőrizzük. A hiányzó él hozzáadása nem módosítja a csomópontok számát, és eggyel növeli az élek és az arcok számát. Euler képlete még mindig ellenőrzött, amely befejezi a demonstrációt.
Grafikonrajz
A most bebizonyított Scheinerman-sejtés szerint minden síkbeli gráf a síkban lévő szegmensek metszéspontjának grafikonja .
Érdeklődés és alkalmazások
Egyszerű példa a síkbeli grafikonok érdeklődésének illusztrálására egy találós kérdés, amelyet három háznak hívnak, amelyet eredetileg matematikai formában HE Dudeney jelentett 1917-ben . Ennek formája a következő: „Három ház lakótelepét vízzel, gázzal és villamos energiával kell felszerelni. A szabályok biztonsági okokból tiltják a csövek keresztezését. Hogyan tegyem? "
Azonban a síkdiagramok iránti érdeklődés régebbi, visszanyúlik a négy szín tételhez . Azóta számos algoritmikusan nehéz ( NP-teljes ) probléma könnyűnek bizonyult ebben a bizonyos osztályban; azonban a legtöbb probléma esetében csak a kisebb K 5 tilalma szükséges.
A síktulajdonság a grafikon felületre történő beágyazódásának ( gráfbeágyazás ) általánosabb kérdésének eredete : beágyazhatunk-e egy adott gráfot egy adott felületre?
A gráf síkbeli tulajdonsága megfizethetőbbé teszi az emberi agy számára amint az a példa a sakk Knight problémát az alábbiakban:
Sakktáblán van egy lovagunk. A cél az, hogy az összes négyzeten átmenjen, csak négyzetenként, tiszteletben tartva a sakk darab klasszikus mozgását. A probléma szemléltetésére itt egy négy négyzetből álló táblát használunk három sorban. A problémát mozgásgráf képviseli; a grafikon csúcsai megfelelnek a sakktábla négyzeteinek; az ívek jelentik a lehetséges mozgásokat. Így az 1. rovatból lehetőség van a 8. vagy a 6. rovatra lépni, mert ezek a grafikon elsőjéhez kapcsolódnak. Az így bemutatott probléma továbbra is összetett. A grafikon azonban sík, és intuitívabban tudjuk ábrázolni. Könnyen kivonhatunk egy új (zöld színnel rajzolt) megoldást a 3. rovatból kiindulva és a 10. rovatig érkezve .A földhözragadt állapotban könnyebb volt megtervezni a legelső tranzisztoros nyomtatott áramköröket, amikor az áramköri grafikon síkbeli volt: ezután elkerültük a kétrétegű folyamatot vagy törékeny " hevedereket ", hogy elkerüljük a nyomtatott áramkör síkját.
Algoritmikus szempontok
Elismerés
Azt a problémát, hogy adott gráf esetén síkgráfról van szó, planaritástesztnek nevezzük . Számos algoritmust javasoltak erre a problémára. A legjobb elérheti a lineáris idő komplexitást , ami aszimptotikailag optimális. Az első ilyen algoritmus 1974-ből származik, és Robert Tarjannak és John Hopcroft-nak köszönhető . Robert Cori a Bulletin de la société informatique de France-ban megjelent cikkében leírta ennek az algoritmusnak a történetét és alapelveit .
Az osztályterembe korlátozott problémák
Bizonyos algoritmikus feladatokat könnyebb megoldani, ha csak sík gráfokra szorítkozunk, például a gráf izomorfizmus problémája lineáris időben megoldható, ami a priori gráfhalmaz esetében eleve nem áll fenn. A közelítéshez hasonlóan például a k-centrum problémát általában nem lehet 2-nél jobb arányban megközelíteni, kivéve, ha P = NP , míg a síkes esetre van egy polinomiális idő-közelítő séma .
Ez nem így van minden problémára, például a vertex lefedettség probléma továbbra is NP-teljes , azaz nehéz megoldani a priori, akkor is, ha korlátozzuk magunkat síkgráfok a foka legfeljebb 3.
Hivatkozások
- Konkrétan Wagner kimutatta, hogy ez a megfogalmazás lehetővé tette az úgynevezett Kisebb tétel megfogalmazását , de mindig azt állította, hogy szerinte kétségtelenül cáfolni fogják.
- T. Chomette, " Planar Graphs " , a CultureMath- on , az École normale supérieure alkalmazott matematikai tanszéke , p. 1 .
- T. Chomette , p. 4.
- (en) Wilfried Imrich és Sandi Klavžar (sl) , Termékgrafikonok : Szerkezet és felismerés , John Wiley & Sons , koll. "Wiley-Interscience sorozat diszkrét matematikában és optimalizálásban",2000.
- A javaslat, valamint a bemutató T. Chomette , p. 3.
- Ez a bemutató T. Chomette- től származik , p. 4.
- (in) Martin Gardner , a hatodik könyve Mathematical Games a Scientific American , University of Chicago Press ,1984( ISBN 0-226-28250-3 ) , p. 92-94
- Úgy találtuk néven „Probléma a három villák és a három gyár” a Claude Berge , Graphes , Gauthier-Villars,1983, 3 e . ( ISBN 978-2-04-015555-1 ) , p. 17.
- John Hopcroft és Robert E. Tarján , „ Efficient sík tesztelés ”, Journal of the ACM , vol. 21, n o 4, 1974, P. 549–568 ( DOI 10.1145 / 321850.321852 ).
- Robert Cori, " A sík vizsgálati algoritmus RE Tarján ", 1024- Bulletin de la Société informatique de France , n o 4,2014. október, P. 55-65 ( ISSN 2270-1419 , online olvasás , konzultáció időpontja : 2020. június 29. ).
- John E. Hopcroft és Jin-Kue Wong , „Lineáris időalgoritmus a síkbeli grafikonok izomorfizmusához” , a hatodik éves ACM szimpózium folyóiratában a számítástechnikáról ,1974( DOI 10.1145 / 800119.803896 ) , p. 172–184.
- Wen-Lian Hsu és George L. Nemhauser, „ Könnyű és nehéz szűk keresztmetszetek elhelyezkedésének problémái ”, Diszkrét alkalmazott matematika , Elsevier, vol. 1, n o 3, 1979, P. 209–215
- David Eisenstat, Philip N. Klein és Claire Mathieu, „Közelítő k- center síkbeli grafikonokban” , a Huszonötödik éves ACM-SIAM szimpózium a diszkrét algoritmusokról, SODA 2014, Portland, Oregon, USA, január 5- 2014. 2014. 7 . 2014, P. 617-627
- (in) Michael Garey és David S. Johnson , Számítógépek és kezelhetetlen: A Guide to the Theory of NP-teljessége , WH Freeman,1979( ISBN 0-7167-1045-5 )
Lásd is
Kapcsolódó cikkek
- Kettős grafikon
- Harc-Harary-Kodama tétel
- Whitney planaritási kritérium
- Fraysseix-Rosenstiehl planaritási kritérium
- Mac Lane planaritási kritérium
- Colin de Verdière planaritási kritérium
- k-fa
Külső linkek
- Algoritmuskönyvtár és grafikonszerkesztő - algoritmusok grafikonja a GPL-ben, beleértve a planaritási tesztet, a síkbeli ábrázolást, a Kuratowski-részgráfok kiállítását lineáris időben
- BGraph - sík grafikonokkal játszani