A Law² törvény nem központosított

Törvény χ 2 nem középen
Valószínűségi sűrűség
Elosztási funkció
Beállítások	k>0{\ displaystyle k> 0 \,}( szabadságfokok ) λ>0{\ displaystyle \ lambda> 0 \,} decentralizációs paraméter
Támogatás	x∈[0;+∞[{\ displaystyle x \ itt: [0; + \ infty [\,}
Valószínűségi sűrűség	12e-(x+λ)/2(xλ)k/4-1/2énk/2-1(λx){\ displaystyle {\ frac {1} {2}} {\ rm {e}} ^ {- (x + \ lambda) / 2} \ bal ({\ frac {x} {\ lambda}} \ jobb) ^ {k / 4-1 / 2} I_ {k / 2-1} ({\ sqrt {\ lambda x}})}
Elosztási funkció	1-Qk2(λ,x){\ displaystyle 1-Q _ {\ frac {k} {2}} \ left ({\ sqrt {\ lambda}}, {\ sqrt {x}} \ right)}a Marcum Q funkció QM(nál nél,b){\ displaystyle Q_ {M} (a, b)}
Remény	k+λ{\ displaystyle k + \ lambda \,}
Variancia	2(k+2λ){\ displaystyle 2 (k + 2 \ lambda) \,}
Aszimmetria	23/2(k+3λ)(k+2λ)3/2{\ displaystyle {\ frac {2 ^ {3/2} (k + 3 \ lambda)} {(k + 2 \ lambda) ^ {3/2}}}}
Normalizált kurtosis	12.(k+4λ)(k+2λ)2{\ displaystyle {\ frac {12 (k + 4 \ lambda)} {(k + 2 \ lambda) ^ {2}}}}
Pillanatgeneráló funkció	exp⁡(λt1-2t)(1-2t)k/2{\ displaystyle {\ frac {\ exp \ balra ({\ frac {\ lambda t} {1-2t}} \ jobbra)} {(1-2t) ^ {k / 2}}}}a t <1/2
Jellemző funkció	exp⁡(énλt1-2ént)(1-2ént)k/2{\ displaystyle {\ frac {\ exp \ balra ({\ frac {i \ lambda t} {1-2it}} \ jobbra)} {(1-2it) ^ {k / 2}}}}

A valószínűségszámítás és a statisztika , a non-központú törvénye χ 2 egy valószínűségi törvény , amely általánosítja a törvény χ² . Ez a törvény statisztikai tesztek során jelenik meg , például a legnagyobb valószínűség érdekében .

Motivációk

Hagyja, X i , k valószın˝uségi változók függetlenek a rendes törvény átlagok és varianciák . Ezután a véletlen változó μén{\ displaystyle \ mu _ {i}}σén2{\ displaystyle \ sigma _ {i} ^ {2}}

∑én=1k(xénσén)2{\ displaystyle \ sum _ {i = 1} ^ {k} \ balra ({\ frac {X_ {i}} {\ sigma _ {i}}} \ jobbra) ^ {2}}

nem központosított χ 2 törvényt követ . Két paramétertől függ: k, amely meghatározza a szabadság fokainak számát (azaz X i számát ), és λ, amely a következő képlettel kapcsolódik az X i változók átlagához :

λ=∑én=1k(μénσén)2.{\ displaystyle \ lambda = \ sum _ {i = 1} ^ {k} \ balra ({\ frac {\ mu _ {i}} {\ sigma _ {i}}} \ jobbra) ^ {2}.}

λ{\ displaystyle \ lambda}néha decentralizációs paraméternek nevezik. Egyes hivatkozások eltérően definiálják a λ-t , például a fenti összeg átlaga vagy annak négyzetgyöke.

Ez a törvény a többváltozós statisztikákban jelenik meg , a többdimenziós normál törvényből származik . Mivel a törvény χ² a négyzete a norma a véletlen vektor meghatározott távolságra a törvény változók (azaz a tér a távolság a származási és egy pont által adott ez a törvény), a törvény a χ 2 nincs középen a négyzete véletlenszerű eloszlási vektor normája . Itt 0 k a nulla vektor hosszúságú k , és azt k az egység mátrix mérete k . NEM(0k,énk){\ displaystyle {\ mathcal {N}} (0_ {k}, I_ {k})}NEM(μ,énk){\ displaystyle {\ mathcal {N}} (\ mu, I_ {k})}μ=(μ1,...,μk){\ displaystyle \ mu = (\ mu _ {1}, ..., \ mu _ {k})}

Meghatározás

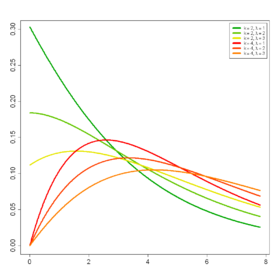
A valószínűségi sűrűséget az alábbiak adják meg:

{fx(x;k,λ)=∑én=0∞e-λ/2(λ/2)énén!fYk+2én(x) ha x>00 ha nem{\ displaystyle {\ begin {cases} f_ {X} (x; k, \ lambda) = \ sum _ {i = 0} ^ {\ infty} {\ dfrac {{\ rm {e}} ^ {- \ lambda / 2} (\ lambda / 2) ^ {i}} {i!}} f_ {Y_ {k + 2i}} (x) és {\ text {si}} x> 0 \\ 0 és {\ text {egyébként}} \ vég {esetek}}}

ahol Y q egy törvénye χ² át q szabadsági fok.

Ebből a reprezentáció, a nem-központú törvénye χ 2 tekintik egy keveréke törvény a törvény . Tegyük fel, hogy a változó J követ Poisson törvény az átlagos λ / 2 , és hogy a feltételes joga a Z tudva J = i a törvény a χ 2 a k +2 i szabadsági fok. Ekkor a Z (feltétel nélküli) törvénye a χ 2 törvénye, amelynek középpontjában nincs k szabadságfok, és a decentralizáció paramétere szerepel . χ2{\ displaystyle \ chi ^ {2}}λ{\ displaystyle \ lambda}

Másrészt a sűrűség formában írható

fx(x;k,λ)=12e-(x+λ)/2(xλ)k/4-1/2énk/2-1(λx){\ displaystyle f_ {X} (x; k, \ lambda) = {\ frac {1} {2}} {\ rm {e}} ^ {- (x + \ lambda) / 2} \ bal ({\ frac {x} {\ lambda}} \ right) ^ {k / 4-1 / 2} I_ {k / 2-1} ({\ sqrt {\ lambda x}})}

ahol I ν ( z ) a módosított Bessel-függvény az első típusú által adott

énnál nél(y)=(y/2)nál nél∑j=0∞(y2/4)jj!Γ(nál nél+j+1).{\ displaystyle I_ {a} (y) = (y / 2) ^ {a} \ sum _ {j = 0} ^ {\ infty} {\ frac {(y ^ {2} / 4) ^ {j} } {j! \ Gamma (a + j + 1)}}.}

A Bessel és a hipergeometrikus függvények kapcsolatát felhasználva a sűrűség a következőképpen is felírható:

fx(x;k,λ)=e-λ/20F1(;k/2;λx/4)12k/2Γ(k/2)e-x/2xk/2-1.{\ displaystyle f_ {X} (x; k, \ lambda) = {{\ rm {e}} ^ {- \ lambda / 2}} _ {0} F_ {1} (; k / 2; \ lambda x / 4) {\ frac {1} {2 ^ {k / 2} \ Gamma (k / 2)}} {\ rm {e}} ^ {- x / 2} x ^ {k / 2-1}. }

Siegel (1979) konkrétabban a k = 0 (0 szabadságfok) esetet veszi figyelembe, ebben az esetben a törvény 0-on atomi.

Tulajdonságok

Pillanatgeneráló funkció

A pillanatgeneráló függvényt az adja

M(t;k,λ)=exp⁡(λt1-2t)(1-2t)k/2.{\ displaystyle M (t; k, \ lambda) = {\ frac {\ exp \ balra ({\ frac {\ lambda t} {1-2t}} \ jobbra)} {(1-2t) ^ {k / 2}}}.}

Pillanatok

Az első pillanatok a következők:

μ1′=k+λ{\ displaystyle \ mu _ {1} ^ {'} = k + \ lambda} μ2′=(k+λ)2+2(k+2λ){\ displaystyle \ mu _ {2} ^ {'} = (k + \ lambda) ^ {2} +2 (k + 2 \ lambda)} μ3′=(k+λ)3+6.(k+λ)(k+2λ)+8.(k+3λ){\ displaystyle \ mu _ {3} ^ {'} = (k + \ lambda) ^ {3} +6 (k + \ lambda) (k + 2 \ lambda) +8 (k + 3 \ lambda)} μ4′=(k+λ)4+12.(k+λ)2(k+2λ)+4(11.k2+44.kλ+36λ2)+48(k+4λ){\ displaystyle \ mu _ {4} ^ {'} = (k + \ lambda) ^ {4} +12 (k + \ lambda) ^ {2} (k + 2 \ lambda) +4 (11k ^ {2 } + 44k \ lambda +36 \ lambda ^ {2}) + 48 (k + 4 \ lambda)}

Az első központosított pillanatok a következők:

μ2=2(k+2λ){\ displaystyle \ mu _ {2} = 2 (k + 2 \ lambda) \,} μ3=8.(k+3λ){\ displaystyle \ mu _ {3} = 8 (k + 3 \ lambda) \,} μ4=12.(k+2λ)2+48(k+4λ){\ displaystyle \ mu _ {4} = 12 (k + 2 \ lambda) ^ {2} +48 (k + 4 \ lambda) \,}

Az n- edik halmozó az

Knem=2nem-1(nem-1)!(k+nemλ).{\ displaystyle K_ {n} = 2 ^ {n-1} (n-1)! (k + n \ lambda). \,}

Így

μnem′=2nem-1(nem-1)!(k+nemλ)+∑j=1nem-1(nem-1)!2j-1(nem-j)!(k+jλ)μnem-j′.{\ displaystyle \ mu _ {n} ^ {'} = 2 ^ {n-1} (n-1)! (k + n \ lambda) + \ sum _ {j = 1} ^ {n-1} { \ frac {(n-1)! 2 ^ {j-1}} {(nj)!}} (k + j \ lambda) \ mu _ {nj} ^ {'}.}

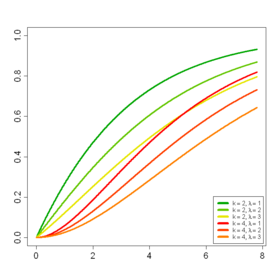
Elosztási funkció

Ismét felhasználva a χ 2 középre és nem központra vonatkozó törvények közötti kapcsolatot , az elosztási függvény formában írható

P(x;k,λ)=e-λ/2∑j=0∞(λ/2)jj!Q(x;k+2j){\ displaystyle P (x; k, \ lambda) = {\ rm {e}} ^ {- \ lambda / 2} \; \ sum _ {j = 0} ^ {\ infty} {\ frac {(\ lambda / 2) ^ {j}} {j!}} Q (x; k + 2j)}

ahol Q ( x  ; k ) a χ 2 törvény eloszlásfüggvénye , k szabadságfokokkal:

Q(x;k)=γ(k/2,x/2)Γ(k/2){\ displaystyle Q (x; k) = {\ frac {\ gamma (k / 2, x / 2)} {\ Gamma (k / 2)}} \,} és ahol γ ( k , z ) a hiányos gammafunkció .

A Marcum Q M ( a , b ) Q függvény felhasználható az eloszlásfüggvény megfogalmazására is:

P(x;k,λ)=1-Qk2(λ,x){\ displaystyle P (x; k, \ lambda) = 1-Q _ {\ frac {k} {2}} \ balra ({\ sqrt {\ lambda}}, {\ sqrt {x}} \ jobbra)}Közelítés

Sankaran az eloszlásfüggvény számos közelítő formáját javasolja. Egy korábbi cikkében a következő kifejezést fogalmazta meg:

P(x;k,λ)≈Φ[(xk+λ)h-(1+ho(h-1-0.5(2-h)mo))h2o(1+0.5mo)]{\ displaystyle P (x; k, \ lambda) \ kb \ Phi \ balra [{\ frac {({\ frac {x} {k + \ lambda}}) ^ {h} - (1 + hp (h- 1 -0,5 (2 órás mp))} {h {\ sqrt {2p}} (1 + 0,5mp)}} \ jobbra]}

vagy

Φ(⋅){\ displaystyle \ Phi (\ cdot) \,}az eloszlásfüggvény a normális eloszlás , h=1-23(k+λ)(k+3λ)(k+2λ)2,{\ displaystyle h = 1 - {\ frac {2} {3}} {\ frac {(k + \ lambda) (k + 3 \ lambda)} {(k + 2 \ lambda) ^ {2}}} \ ,,} o=k+2λ(k+λ)2,{\ displaystyle p = {\ frac {k + 2 \ lambda} {(k + \ lambda) ^ {2}}},} m=(h-1)(1-3h).{\ displaystyle m = (h-1) (1-3h) \,.}

Ez a közelítés és mások egy későbbi könyvben szerepelnek.

A χ 2 törvényének megközelítéséhez a λ decentralizációs paraméter nulla.

Kapcsolat más törvényekkel

• Ha V a chi-négyzet eloszlás , míg szintén joga χ 2 nem középen: .V∼χk2{\ displaystyle V \ sim \ chi _ {k} ^ {2}}V{\ displaystyle V}V∼χ′k2(0){\ displaystyle V \ sim {\ chi '} _ {k} ^ {2} (0)}
• Ha , és V 1 és V 2 függetlenek, így a Fisher-féle nem középen  : .V1∼χ′k12(λ){\ displaystyle V_ {1} \ sim {\ chi '} _ {k_ {1}} ^ {2} (\ lambda)}V2∼χ′k22(0){\ displaystyle V_ {2} \ sim {\ chi '} _ {k_ {2}} ^ {2} (0)}V1/k1V2/k2{\ displaystyle {\ frac {V_ {1} / k_ {1}} {V_ {2} / k_ {2}}}}V1/k1V2/k2∼Fk1,k2′(λ){\ displaystyle {\ frac {V_ {1} / k_ {1}} {V_ {2} / k_ {2}}} \ sim F '_ {k_ {1}, k_ {2}} (\ lambda)}
• Ha , ahol Poisson-eloszlást jelöl , akkorJ∼P(λ2){\ displaystyle J \ sim {\ mathcal {P}} ({\ frac {\ lambda} {2}})}P{\ displaystyle {\ mathcal {P}}}χk+2J2∼χ′k2(λ){\ displaystyle \ chi _ {k + 2J} ^ {2} \ sim {\ chi '} _ {k} ^ {2} (\ lambda)}
• Közelítés a szokásos gyakorlat: ha , akkor a valószínűség , ha vagy .V∼χ′k2(λ){\ displaystyle V \ sim {\ chi '} _ {k} ^ {2} (\ lambda)}V-(k+λ)2(k+2λ)→NEM(0,1){\ displaystyle {\ frac {V- (k + \ lambda)} {\ sqrt {2 (k + 2 \ lambda)}}} \ - {\ mathcal {N}} (0,1)}k→∞{\ displaystyle k \ to \ infty}λ→∞{\ displaystyle \ lambda \ to \ infty}

Átalakulások

Sankaran (1963) a forma átalakulásait tanulmányozza . Elemzi a z nagyságrendű z kumulánsok fejlődését, és megmutatja, hogy b következő választásai a következő ésszerű eredményeket adják: z=[(x-b)/(k+λ)]1/2{\ displaystyle z = [(Xb) / (k + \ lambda)] ^ {1/2}}O((k+λ)-4){\ displaystyle O ((k + \ lambda) ^ {- 4})}

• b=(k-1)/2{\ displaystyle b = (k-1) / 2}a z második kumulánsát megközelítőleg függetlenné teszi λ-tól ,
• b=(k-1)/3{\ displaystyle b = (k-1) / 3}a z harmadik kumulánsát megközelítőleg függetlenné teszi λ-tól ,
• b=(k-1)/4{\ displaystyle b = (k-1) / 4}a z negyedik kumulátumát megközelítőleg független λ-tól .

Ezenkívül egy egyszerűbb transzformáció is alkalmazható varianciastabilizáló függvényként, amely véletlenszerű változót és varianciát eredményez . z1=(x-(k-1)/2)1/2{\ displaystyle z_ {1} = (X- (k-1) / 2) ^ {1/2}}(λ+(k-1)/2)1/2{\ displaystyle (\ lambda + (k-1) / 2) ^ {1/2}}O((k+λ)-2){\ displaystyle O ((k + \ lambda) ^ {- 2})}

Ezen transzformációk használatát befolyásolhatja a negatív számok négyzetgyökének figyelembevétele.

A χ és χ 2 különböző törvényei

Törvények	a normális eloszlási változók függvényében
törvény χ²	∑én=1k(xén-μénσén)2{\ displaystyle \ sum _ {i = 1} ^ {k} \ balra ({\ frac {X_ {i} - \ mu _ {i}} {\ sigma _ {i}}} \ jobbra) ^ {2} }
law² törvény nem központosított	∑én=1k(xénσén)2{\ displaystyle \ sum _ {i = 1} ^ {k} \ balra ({\ frac {X_ {i}} {\ sigma _ {i}}} \ jobbra) ^ {2}}
törvény χ	∑én=1k(xén-μénσén)2{\ displaystyle {\ sqrt {\ sum _ {i = 1} ^ {k} \ bal ({\ frac {X_ {i} - \ mu _ {i}} {\ sigma _ {i}}} \ jobb) ^ {2}}}}
törvény a χ nem központosított	∑én=1k(xénσén)2{\ displaystyle {\ sqrt {\ sum _ {i = 1} ^ {k} \ balra ({\ frac {X_ {i}} {\ sigma _ {i}}} \ jobbra) ^ {2}}}}

Hivatkozások

1. Muirhead (2005) 1.3.4. Tétel
2. Nuttall, Albert H. (1975): Néhány integrál, amely bevonja a Q M funkciót , IEEE tranzakciók az információelméletről , 21 (1), 95-96, ( ISSN  0018-9448 )
3. Sankaran, M. (1963). Közelítések a nem központi chi-négyzet eloszláshoz Biometrika , 50 (1-2), 199–204
4. Sankaran, M. (1959). "A nem központi chi-négyzet eloszlásról", Biometrika 46, 235–237
5. Johnson és mtsai. (1995) 29.8. Szakasz
6. Muirhead (2005) 22–24. Oldal és 1.18.

• Abramowitz, M. és Stegun, IA (1972), Matematikai függvények kézikönyve , Dover. Szakasz: 26.4.25.
• Johnson, NL, Kotz, S., Balakrishnan, N. (1970), Continuous Univariate Distributions, 2. kötet , Wiley. ( ISBN  0-471-58494-0 )
• Muirhead, R. (2005) A többváltozós statisztikai elmélet szempontjai (2. kiadás). Wiley. ( ISBN  0471769851 )
• Siegel, AF (1979), "A nem centrális chi-négyzet eloszlás nulla szabadságfokkal és az egyenletesség tesztelése", Biometrika , 66, 381–386

<img src="https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">