Alapvető csoport

A matematika , pontosabban algebrai topológia , az alapvető csoport , vagy Poincaré-csoport , egy topológiai invariáns . Az alapvető csoport egy hegyes topologikus tér ( X, p ), meghatározás szerint, a készlet homotopy osztályok a hurkok ( zárt pályák ) a X bázissal p . Ez egy olyan csoport, amelynek belső összetételének törvényét az ívek összefűzése (egymás mellé helyezése) indukálja .

Az alapvető csoportok vizsgálata lehetővé teszi annak bizonyítását, hogy két meghatározott tér nem lehet homeomorf (azaz topológiailag egyenértékű). Az alapcsoport lehetővé teszi egy összekapcsolt tér burkolatainak ívek szerinti osztályozását , egy izomorfizmusig .

Az alapvető csoportok általánosítása a magasabb homotópiás csoportok folytatása . Emiatt az alapcsoportot első homotópiás csoportnak is nevezik .

Az alapcsoportot Henri Poincaré mutatta be az 1895-ben megjelent Analysis Situs című cikkének tizenkettedik részében , amelyet az 1892-ben megjelent Tudományos Akadémia jelentéseihez közöltek.

Intuitív definíció a tórus példáján keresztül

Először ismerkedjünk meg az alapcsoport eszméjével a kétdimenziós tórus példáján keresztül (amely felfogható fánk vagy bója felületének ). A tóruszra rögzítünk egy p kezdőpontot .

Innentől kezdve csipkéket , azaz zárt görbéket készíthetünk , amelyek a p ponttól indulnak , „járnak” a tóruson és visszatérnek a kiindulási pontra. Képzelje el, hogy a csipkék gumiból készülnek, mint egy elasztikusak, és így meg lehet őket nyújtani, deformálni úgy, hogy a kiindulási és a végpont mindig p legyen, és a csipkék mindig a tóruson mozogjanak. Az ilyen alakváltozást homotopiának nevezzük  : azt mondjuk, hogy két hurok, amelyet homotópiával lehet egymásból megszerezni, homotópiailag ekvivalens. A deformációig tartó csipkék érdekelnek bennünket: ezért a csipkéket homotópia osztályokba csoportosítjuk. A tórusz alapvető csoportja a csipkék különböző homotópiaosztályainak halmaza.

A szemközti ábrán az a és b hurok nem homotópiailag egyenértékű: az egyiket nem lehet úgy megszerezni, hogy folyamatosan deformáljuk a másodikat anélkül, hogy egyszerre „elszakítanánk”, az alapcsoport két elkülönített elemét képviselik. A homotopia más osztályait úgy kapjuk meg, hogy a csipkéket többször elforgatjuk a lyuk körül.

Ahogy a neve is sugallja, az alapcsoport nem egyszerű halmaz, hanem csoportszerkezettel rendelkezik  : a belső összetétel törvénye az, amely két hurokkal társítja az első, majd a második áthaladásával kapott harmadik hurkot (nincsenek problémák meghatározása, mivel a csipkék ugyanazzal a p ) ponttal kezdődnek és végződnek . A semleges eleme az alapvető csoport a homotopy osztály a legyezési amely továbbra pontban p . Az inverz elemet úgy kapjuk meg, hogy a homotópia osztály fűzőit ellentétes irányban haladjuk át.

Meghatározás

Csipkék egyenértékűségi osztálya

Legyen X topológiai tér. A folyamatos ív egy folytonos γ  : [0 1] → X .

Legyen p egy fix pont X-ben . A legyezési alapuló p egy folyamatos ív további kielégítő γ (0) = γ (1) = p . Úgy értelmezhető, mint a folyamatos térképét a készülék körben S 1 az X , amely elküldi 1. o .

Két γ 0 és γ 1 hurokról azt mondják, hogy homotóp, ha van homotópia egyikről a másikra, azaz egy folytonos H térkép  : [0 1] 2 → X oly módon, hogy:

• ∀t∈[0,1],H(t,0)=γ0(t){\ displaystyle \ összes t \ -ban [0,1], \, H (t, 0) = \ gamma _ {0} (t)}
• ∀t∈[0,1],H(t,1)=γ1(t){\ displaystyle \ összes t \ -ban [0,1], \, H (t, 1) = \ gamma _ {1} (t)}
• ∀x∈[0,1],H(0,x)=o=H(1,x).{\ displaystyle \ forall x \ in [0,1], \, H (0, x) = p = H (1, x).}

Az utolsó feltétel azt fejezi ki, hogy a 0 és 1 között rögzített x esetében a t ↦ H ( t , x ) egy p alapú hurok .

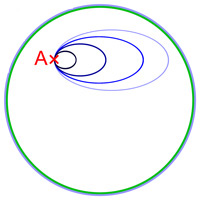
Más szavakkal, két hurokról azt mondják, hogy homotóp, ha folyamatosan haladhatunk egyikről a másikra, mint a jobb oldali ábra (a p pont az A-n található az ábrán).

A homotóp lét ekvivalencia viszony a hurkok között ( p alapján ). Mi jelöljük [ γ ] ekvivalencia osztály egy legyezési γ (más néven homotopy osztály).

A beállított π 1 ( X , p ) ilyen ekvivalencia osztályok azonosították a készlet komponenseket összekötött ívek a tér hurkok alapuló p a X (ellátva kompakt nyitott topológia ), jele Ω ( X , p ), és az a csoportstruktúra, amellyel az alábbiakban közöljük, valójában az Ω ( X , p ) H-csoport szerkezetéből származik :

π1(x,o)=π0(Ω(x,o)).{\ displaystyle \ pi _ {1} (X, p) = \ pi _ {0} (\ Omega (X, p)).}

A csoport felépítése

Ennek a π 1 ( X , p ) halmaznak csoportszerkezetet akarunk adni . Ha f és g két hurok X (székhelyű p ), azok egymás mellé , vagy összetételét a csipkés H úgynevezett csipkés álló az f és g vagy terméket csipkés fg , által meghatározott:

h(t)={f(2t),ha t∈[0,1/2]g(2t-1),ha t∈[1/2,1]{\ displaystyle h (t) = \ left \ {{\ begin {mátrix} f (2t), & {\ mbox {si}} t \ in [0,1 / 2] \\ g (2t-1), & {\ mbox {si}} t \ in [1 / 2,1] \ end {mátrix}} \ right.}

Intuitív módon az áthajlás az, ami áthalad f, majd g (mindegyik kétszer olyan gyorsan, hogy egységnyi idő alatt sikerül áthaladni a kanyarban). Fg-vel jelöljük az f és g vegyületet . Bebizonyíthatjuk, hogy a [ fg ] homotópia osztály csak az f , és a g homotópiás osztályától függ . Így tudjuk határozni egy belső készítmény törvény a beállított π 1 ( X , p ) a homotopy osztályok hurkok székhelyű p az X , az [ f ] [ g ] = [ fg ], más néven egymás mellé .

Ezután be tudjuk bizonyítani, hogy a π 1 ( X , p ) halmazon csoportszerkezetet kapunk :

• a szembeállítás törvénye asszociatív, mert a hurkok ( fg ) h és f ( gh ) homotópok,
• a semleges elem a triviális hurok γ homotopia osztálya [ γ ], amelyet γ ( t ) = p határoz meg minden t-re .
• Az f hurok inverze egyszerűen ugyanaz a hurok, de áthalad a másik irányba, vagyis az f −1 ( t ) = f (1 - t ).

A csoport így kapott nevezzük az alapvető csoport , vagy a Poincaré-csoport , vagy az első homotopy csoport a X alapuló p , és jelöljük π 1 ( X , p ).

Ha X a p semleges elem topológiai csoportja (vagy általánosabban H-tér  (en) ) , akkor a π 1 ( X , p ) csoport abeli és az összetett fg hurok homotópikus a t ↦ f ( t ) g ( t ).

Alappont

Nézzük az esetben, ha a topológiai tér X van összekötve ívek . Két p és q ponton alapuló két alapvető csoport ( π 1 ( X , p ) és π 1 ( X , q )) izomorf. Sőt, van egy út γ haladva p a q . Ezért meghatározhatjuk a következő alkalmazást

[α]↦[γ][α][γ]-1{\ displaystyle [\ alpha] \ mapsto [\ gamma] [\ alpha] [\ gamma] ^ {- 1}}

amely láthatóan megvalósítja az izomorfizmust a π 1 ( X , q ) alapcsoporttól a π 1 ( X , p ) alapcsoportig , amelynek kölcsönös izomorfizmusa az alkalmazás:

[α]↦[γ]-1[α][γ]{\ displaystyle [\ alpha] \ mapsto [\ gamma] ^ {- 1} [\ alpha] [\ gamma]}

Így, ha X csatlakozik ívek, a visszaélés a nyelv, beszélünk az alapvető csoport ( kivéve a nem egyedi izomorfizmus) a topologikus tér X , megadása nélkül a bázis pont, amely mi jelöljük π 1 ( X ) = π 1 ( X , p ). Az π 1 ( X , p ) és a π 1 ( X , q ) csoportok közötti izomorfizmus azonban nem egyedi, és függ a p és q közötti út választásától . Tehát emlékeznünk kell arra, hogy az alapcsoport változik, ha az alaptér az X térben változik , a csoportok mindig izomorfok maradnak.

Ha X- et nem ívek kötik össze, akkor két összekapcsolt komponens alapvető csoportjai különbözőek. A nyelvvel való visszaélés ellenére mindazonáltal az ívekkel összekötött komponens alapvető csoportjáról beszélünk, anélkül, hogy meghatároznánk az alappontot, de emlékeznünk kell arra, hogy az alapcsoport akkor változik, amikor az alappont változik az ívekkel összekötött komponensben, a csoportok mindig megmaradnak izomorf.

Példák

Egyszerűen kapcsolódó terek

A triviális alapvető csoportívekkel összekötött teret állítólag egyszerűen összekötik .

Például bármilyen kontraktilis térben (azaz amelyek visszahúzódik deformálásával egy pont) és különösen az olyan konvex a ℝ n , egyszerűen csatlakoztatva. A gömb S n az n ≥ 2 is egyszerűen csatlakoztatva.

Kör

A kifejezés kör jelöl itt teret homeomorf egy kört az az euklideszi sík , mint a hányadost topologikus csoport ℝ / ℤ vagy mint a készülék körhöz S 1 a komplex számok modulus 1.

• A kör alapcsoportja izomorf az egész számok ℤ csoportjával szemben .

(Ez a gömbök homotópiai csoportjainak speciális esete  : π n ( S n ) = ℤ.)

Itt figyelembe vesszük π 1 ( S 1 , 1), vagyis az alappont 1. Meghatározzuk a π 1- ből μ-től μ-ig terjedő csoportok morfizmusát ( S 1 , 1), amelyek minden m egész számhoz társítják a osztályú csipke e m, amely | m | fordul, az óramutató járásával ellentétes irányba, ha m pozitív, és az óramutató járásával ellentétes irányba: em:[0,1]→S1em(t)=exp⁡(2énπmt).{\ displaystyle e_ {m}: [0,1] \ rightarrow S ^ {1} \ quad e_ {m} (t) = \ exp (2 \ mathrm {i} \ pi mt).} Valóban morfizmus, mert az e m e n összetett csipke homotóp a termék csipkével, egyenlő e m + n-vel . Annak megállapításához, hogy ez bijektív, be kell mutatnunk, hogy a „fordulatok száma” jól meghatározható minden ívnél és csak annak homotópiás osztályától függ, és hogy minden m-es fordulatot végrehajtó ás homotópikus e m-rel .

A számítás részletei

A probléma egy inverz szerkesztése  : μ{\ displaystyle \ mu}

v:π1(S1)→Z.{\ displaystyle \ nu: \ pi _ {1} (S ^ {1}) \ to \ mathbb {Z}.}

Ehhez egy p alkalmazást határozunk meg:

o:R→S1o(t)=exp⁡(2énπt).{\ displaystyle p: \ mathbb {R} \ rightarrow S ^ {1} \ quad p (t) = \ exp (2 \ mathrm {i} \ pi t).}

A bizonyításhoz szükséges lemma megállapításához hasznos egy megjegyzés. Az e 1 intervallumra való korlátozása ] –1/2, 1/2 [egy homeomorfizmus, amelynek értéke S 1 \ {- 1}; a jobb oldali ábra szemlélteti. A bijektív karakter nyilvánvaló, a korlátozás folyamatos és inverz σ folyamatos, mert a következő határozza meg:

∀z∈S1∖{-1},z=x+ényσ(z)=1πarctan⁡(y1+x){\ displaystyle \ forall z \ in S ^ {1} \ setminus \ {- 1 \}, \; z = x + iy \ quad \ sigma (z) = {\ frac {1} {\ pi}} \ arctan \ balra ({\ frac {y} {1 + x}} \ jobbra)}

• Tartozó tétel  : Legyen α: [0, 1] → S 1 olyan folytonos térkép, hogy α (0) = 1. Létezik egy egyedi β folytonos térkép: [0, 1] → ℝ úgy, hogy β (0) = 0 és p ∘ β = α:

Hadd állapítsuk meg a β egyediségét. Legyen β 1 és β 2 két térkép, amely kielégíti az állítást. Különbségük nulla, mert folytonos, 0 nulla, egy kapcsolaton definiálva, és diszkrét halmaz értékeivel (ebben az esetben ℤ).

Mutassuk meg a létezését. Ha az α értéke S 1 \ {- 1}, akkor az a tény, hogy σ homeomorfizmus, arra enged következtetni. Ha nem ez a helyzet, akkor a [0, 1] intervallum „felosztásával” folytatjuk. Az α térkép tömören definiált és folyamatos; ezért egységesen folyamatos , ami egy szigorúan pozitív valós r létét mutatja , amely:

∀t1,t2∈[0,1]|t1-t2|<r⇒|α(t1)-α(t2)|<2 vagy |α(t2)α(t1)-1|<2 mivel |α(t1)|=1.{\ displaystyle \ összes t_ {1}, t_ {2} \ in [0,1] \ quad | t_ {1} -t_ {2} | <r \ Rightarrow | \ alpha (t_ {1}) - \ alpha (t_ {2}) | <2 {\ text {vagy ismét}} \ balra | {\ frac {\ alpha (t_ {2})} {\ alpha (t_ {1})}} - 1 \ jobbra | < 2 {\ text {autó}} | \ alfa (t_ {1}) | = 1.}

Vagyis, ha eltér szigorúan kisebbtől , akkor az arány soha nem éri el a -1 értéket, ami nincs meghatározva. Ez a tulajdonság a funkció szakaszos definiálására szolgál . Legyen M szigorúan pozitív egész szám, amely 1 / M szigorúan kisebb, mint . A [0, 1 / M ] intervallum alatt a függvényt egyenlőnek definiáljuk . Van egyenlőségünk t2{\ displaystyle t_ {2}}t1{\ displaystyle t_ {1}}r{\ displaystyle r}α(t2)/α(t1){\ displaystyle \ alpha (t_ {2}) / \ alpha (t_ {1})}σ{\ displaystyle \ sigma}β{\ displaystyle \ beta}r{\ displaystyle r}β{\ displaystyle \ beta}σoα{\ displaystyle \ sigma o \ alfa}

∀t∈[0,1/M]β(t)=σ∘α(t)éso∘β(t)=α(t){\ displaystyle \ forall t \ in [0,1 / M] \ quad \ beta (t) = \ sigma \ circ \ alfa (t) \ quad {\ text {et}} \ quad p \ circ \ beta (t ) = \ alfa (t)}

Legyen k egész szám 1 és , és . A [ k / M , ( k + 1) / M ] intervallumon belül a t- vel társított függvény egyenlő 1 k / M-ben, és képei soha nem hagyják el a definíció tartományát . Ezt a helyzetet szemlélteti a jobb oldali ábra, minden szegmensnél a csipke más színű, egyetlen szegmens sem tér el pontosan fél fordulattal a kiindulási ponttól. Ez lehetővé teszi a következő intervallumon történő meghatározást: M-1{\ displaystyle M-1}αk=α(k/M)-1{\ displaystyle \ alpha _ {k} = \ alpha (k / M) ^ {- 1}}αk.α(t){\ displaystyle \ alpha _ {k}. \ alpha (t)}σ{\ displaystyle \ sigma}β{\ displaystyle \ beta}

∀t∈[k/M,(k+1)/M]β(t)=σ(αkα(t))+β(k/M){\ displaystyle \ összes t \ itt: [k / M, (k + 1) / M] \ quad \ beta (t) = \ sigma \ bal (\ alfa _ {k} \ alfa (t) \ jobb) + \ béta (k / M)}

Konstrukció szerint a funkció folyamatos, és k indukciójával kielégíti a keresett egyenlőséget: β{\ displaystyle \ beta}

∀t∈[k/M,(k+1)/M]o∘β(t)=o∘(σ(αkα(t)))⋅o∘β(k/M)=αkα(t)α(k/M)=α(t).{\ displaystyle \ forall t \ itt: [k / M, (k + 1) / M] \ quad p \ circ \ beta (t) = p \ circ (\ sigma \ left (\ alpha _ {k} \ alpha ( t) \ jobbra)) \ cdot p \ circ \ beta (k / M) = \ alfa _ {k} \ alfa (t) \ alfa (k / M) = \ alfa (t).}

Most azt feltételezzük, hogy ez egy csipke. Az alkalmazást úgy definiáljuk, mint amely a véget társítja , amely intuitívan megfelel az elvégzett fordulatok számának . Mivel egyenlő 1-vel, egész szám. α{\ displaystyle \ alpha}v{\ displaystyle \ nu}α{\ displaystyle \ alpha}β(1){\ displaystyle \ beta (1)}α{\ displaystyle \ alpha}α(1){\ displaystyle \ alpha (1)}v(α){\ displaystyle \ nu (\ alpha)}

Még mindig be kell mutatni, hogy az alkalmazás kompatibilis a homotópiával. Az első lemma hasznos. v{\ displaystyle \ nu}

• Ha az 1. bázis S 1 két α 1 és α 2 hurka igazolja a következő növekedést, akkor ugyanaz a képük  :v{\ displaystyle \ nu}

∀t∈[0,1]|α1(t)-α2(t)|<2{\ displaystyle \ összes t \ -ban [0,1] \ quad | \ alpha _ {1} (t) - \ alpha _ {2} (t) | <2}

Megvizsgáljuk a hányados alkalmazást . Képét az S 1 \ {- 1} tartalmazza, vagyis a definíció tartománya . A csapágy egyedisége alapján a szokásos jelölésekkel következtethetünk: αvs.=α1/α2{\ displaystyle \ alpha _ {c} = \ alpha _ {1} / \ alpha _ {2}}σ{\ displaystyle \ sigma}

β1-β2=βvs.=σ∘αvs.{\ displaystyle \ beta _ {1} - \ beta _ {2} = \ beta _ {c} = \ sigma \ circ \ alpha _ {c}}

különösen

v(α1)-v(α2)=β1(1)-β2(1)∈Z∩énm(σ)=Z∩]-12,12[={0}.{\ displaystyle \ nu (\ alpha _ {1}) - \ nu (\ alpha _ {2}) = \ beta _ {1} (1) - \ beta _ {2} (1) \ in \ mathbb {Z } \ cap {\ rm {im}} (\ sigma) = \ mathbb {Z} \ cap \ left] - {\ tfrac {1} {2}}, {\ tfrac {1} {2}} \ right [ = \ {0 \}.}

• Legyen α 1 és α 2 az S 1 két hurka az 1. bázissal és a homotópokkal. Ugyanaz a képük  :v{\ displaystyle \ nu}

Legyen H olyan hurkok homotópiája, amelyeknek az alapja 1- től kezdve . A kompakt [0, 1] 2 folytonos H térkép egyenletesen folytonos. Ezért van egy M egész szám , amely: α1{\ displaystyle \ alpha _ {1}}α2{\ displaystyle \ alpha _ {2}}

∀k∈{1,⋯M},∀t∈[0,1]|H(t,(k-1)/M)-H(t,k/M)|<2{\ displaystyle \ összes k \ -ban \ {1, \ cdots M \}, \; \ összes t \ -ban [0,1] \ quad | H (t, (k-1) / M) -H (t, k / M) | <2}

Az előző lemma szerint a H (, 0 / M ), H (, 1 / M ), H (, 2 / M ),…, H (, M / M ) hurkok mindegyike azonos képpel rendelkezik . Az első és az utolsó α 1 és α 2 . v{\ displaystyle \ nu}

• Következtetés  :

Mi már jól definiált egy térképet a π 1 ( S 1 , 1) a ℤ, kielégítő az építőipar . Ezt még be kell mutatni . Hagyd és . A térkép ( t , x ) ↦ p ((1 - x ) β ( t ) + xmt ) ekkor homotópiát hajt végre α-tól e m-ig . v{\ displaystyle \ nu}v∘μ=éndZ{\ displaystyle \ nu \ circ \ mu = {\ rm {id}} _ {\ mathbb {Z}}}μ∘v=éndπ1(S1){\ displaystyle \ mu \ circ \ nu = {\ rm {id}} _ {\ pi _ {1} (S ^ {1})}}[α]∈π1(S1){\ displaystyle [\ alpha] \ in \ pi _ {1} (S ^ {1})}m=v([α])=β(1){\ displaystyle m = \ nu ([\ alpha]) = \ béta (1)}

A kör alapvető csoportjának nem triviális volta a nem triviális tételek több bizonyításának eredetét képezi. Ilyen például a Borsuk-Ulam, amely azt jelzi, hogy a gömb folyamatos alkalmazása a síkban mindig két antipodális ponttal rendelkezik, azonos képpel. Ez az eredmény a kulcsa a sonkás szendvics-tétel bizonyításának, amely azt jelzi, hogy mindig létezik egy sík, amely azonos térfogatú két részre oszlik, három kötött és mérhető szilárd anyagra.

Termékterület

Ha ( X i ) egy családi kapcsolódó területek által ívek, a terméket térben X = Π X i van útvonal csatlakozik, így az alapvető csoport független a talppont kiválasztott X . Továbbá:

Az alapvető csoportja a termék tér Π X i jelentése a közvetlen termék alapvető csoportok X i .

Ez azonnal a univerzális tulajdonság a termék: az adatok folyamatos térképet Y a Π X i jelentése megegyezik a család folyamatos térképek az Y minden egyes X i , bármilyen tér Y , különösen S 1 és S 1 × [0, 1].

Például az n -tore alapvető csoportja T n = ( S 1 ) n izomorf a to n szabad abeli csoporttal szemben .

Egyéb példák

• Az alapcsoport tartalmazhat torziós elemeket  : például a valós projektív sík P 2 (ℝ) alapcsoportja izomorf a ℤ / 2ℤ-vel (lásd alább ).
• Az alapcsoport nem mindig kommutatív: például a két ℝ 2 \ { a , b } ponttól megfosztott sík p pontján alapuló alapcsoport izomorf a két F 2 generátorral rendelkező szabad csoportra . A két generátor itt hurok kezdődik p- től kezdve, és mindegyik megkerüli az a vagy b pontok egyikét .

Tétel Bármely G csoport esetében van egy topológiai tér, amelynek G alapcsoportja van . Megtalálható valójában egy kétdimenziós CW komplex, vagy akár a 4 (in) dimenzió sokféle változata , ha a csoport átmegy . 

Folyamatos működés és morfizmus

A természetes kérdés az, hogy a kompatibilitás alapvető csoport tekintetében folyamatos alkalmazás f . Legyen X és Y két topologikus terek úgy, hogy X kapcsolódik az ARC és f folyamatos feltérképezése X a Y . Az f függvény nemcsak az f ( X ), hanem az ívekkel való összeköttetését is biztosítja.

Ezenkívül az f függvény átalakítja az X szöget egy Y szögben . Α X szög , az f ∘α alkalmazás Y Y kúp . Ezt a csipkét általában f ✻ (α) -nak jelöljük .

Az alapvető csoportok morfizmusa, amelyet folyamatos funkció indukál

A függvény f indukál f ✻ fűzők X a csipkék az Y . Ez az alkalmazás kompatibilis a homotópia által meghatározott egyenértékűségi relációval, valamint az alapcsoport összetételének törvényével.

Ha α 1 és α 2 a p bázis két hurka , akkor az egymás mellé helyezés törvénye érvényes. Ha a két hurok homotóp által H , akkor a térkép f ∘ H egy homotopy közötti f ✻ (α 1 ) és f ✻ (α 2 ), ami azt mutatja, hogy a térkép f ✻ van definiálva a csoport π 1 ( X , p ) az π 1 ( Y , f ( p )) csoport értékeivel . Továbbá:

• A térkép f ✻ , a π 1 ( X , p ) a tc 1 ( Y , F ( p )) , által meghatározott:∀[γ]∈π1(x,o),f∗([γ])=[f∘γ]{\ displaystyle \ forall [\ gamma] \ in \ pi _ {1} (X, p), \ quad f _ {*} ([\ gamma]) = [f \ circ \ gamma]} egy morfizmus csoportok . Ezt a morfizmust nevezzük az f alkalmazás által kiváltott morfizmusnak .

Ha Z egy másik topológiai tér és g folytonos függvény Y- től Z-ig , akkor a morfizmusok a következőkből állnak:

(g∘f)∗=g∗∘f∗.{\ displaystyle (g \ circ f) _ {*} = g _ {*} \ circ f _ {*}.}

Elég észrevenni, hogy a térkép (Id X ) ✻ a π 1 ( X , p ) csoport azonossága annak megállapítására, hogy:

• Ha f homeomorfizmus, akkor az f ✻ csoportmorfizmus izomorfizmus.

Ha két teret ívek kötnek össze és homeomorfak, akkor alapvető csoportjaik izomorfak. Az izomorfizmus általában nem egyedi.

Alkalmazás: Brouwer fixpont tétel a 2. dimenzióban

Az előző morfizmusok alkalmazására példa a Brouwer-féle fixpont-tétel. A 2. dimenzióban egyszerűen egy folyamatos funkció tanulmányozásával mutatják be, amely lehetővé teszi az alapvető csoportok morfizmusának felépítését. A meghatározás hasznos:

Hadd X egy topologikus tér és az útvonal csatlakozik egy része X . A visszahúzás származó X , hogy egy folytonos térképet X az A , akinek korlátozás A identitás. Azt mondjuk, hogy egy olyan visszahúzás az X , ha van egy visszahúzó X -ra egy .

Ez a meghatározás lehetővé teszi számunkra, hogy a következő javaslatot fejezzük ki, ami egyenértékű Brouwer fixpontos tételével a 2. dimenzióban:

• A határán nincs visszahúzva egy lemez.

Legyen B 2 a lemez és S 1 a szegélye. Tegyük fel, hogy létezik ilyen visszahúzás, amelyet F jelez a B 2-től az S 1-re . Jelölje Inj S kanonikus injekció S 1 a B 2 és Id S a személyazonosságát feltérképezése a S 1 . Ekkor a következő ellentmondásunk lesz:

IdZ=(IdS)∗=(F∘InjS)∗=F∗∘(InjS)∗=F∗∘0=0,{\ displaystyle {\ text {Id}} _ {\ mathbb {Z}} = ({\ text {Id}} _ {S}) _ {*} = (F \ circ {\ text {Inj}} _ { S}) _ {*} = F _ {*} \ circ ({\ text {Inj}} _ {S}) _ {*} = F _ {*} \ circ 0 = 0,}

az a tény, hogy a morfizmus (inj S ) ✻ nulla hogy igazolja az a megjegyzéssel, hogy az értékek az alapvető csoport a lemez, ami triviális.

A Brouwer tétel kimondja, hogy minden folytonos függvény f A lemez maga is elismeri, a fix pont. Ha nem lenne, akkor könnyű lenne visszahúzást építeni. Figyelembe vennénk az ábrán bemutatott x-en és f ( x ) -en áthaladó szegmenst (ha x a lemez eleme). Ez a szakasz keresztezi a lemezt egy pontban, közelebb x-hez, mint f ( x ) -hez . Ha ez a pont az x pont F képe , akkor F a kívánt visszahúzás. Pontosabb leírás a részletes cikkben található:

Egyéb tételek

Két X és Y topológiai teret homotóp ekvivalensnek nevezünk, ha két folytonos f térkép van  : X → Y és g  : Y → X úgy, hogy g ∘ f homotópikus legyen az id X- del, és f ∘ g homotópikus legyen az id Y-vel .

Ha két teret ívek kötnek össze és homotóposan ekvivalensek, akkor alapvető csoportjaik izomorfak.

Például egy egyszerűen összekapcsolt térrel homotopilag egyenértékű tér egyszerűen összekapcsolódik.

Tulajdonságok

Kapcsolat az első homológiai csoporttal

Az első homológia csoport egy tér van a közvetlen összege az első homológ csoportok egyes alkotóelemek összekötött ívek. Hurewicz tételének egy speciális esete a komponensek homológiájának ezeket a csoportjait kapcsolja az alapvető csoportjaikkal:

Az ívekkel összekötött tér első teljes homológiai csoportja izomorf az alapcsoportjának abelianizálódásával szemben.

Alapcsoport- és bevonatelmélet

Az alcsoportok közötti egyenértékűség konjugációval az alapcsoport közelében és az izomorfizmusig terjed . Ebben az egyenértékűségben a normál alcsoportok megfelelnek a Galois-burkolatoknak.

A burkolatelméletben megmutatjuk, hogy ha a tér egyszerűen összekapcsolt burkolatot enged meg (különösen, ha a tér félig lokálisan egyszerűen kapcsolódik, vagyis ha a tér nem túl "  vad  ", például ha lokálisan összehúzódik) alapvető csoportja izomorf az egyik univerzális burkolatának automorfizmusaihoz képest.

Számítási módszerek és alkalmazások

Van Kampen tétele

A nem egyszerűen összekapcsolt topológiai tér alapvető csoportjának kiszámítása nehéz feladat, mert be kell bizonyítani, hogy egyes hurkok nem homotópok. A van Kampen-tétel , más néven Seifert-Van Kampen-tétel , megoldja ezt a problémát, amikor a topológiai tér egyszerűbb terekké bontható, amelyek alapvető csoportjai már ismertek. Ez a tétel lehetővé teszi számunkra, hogy kiszámoljuk a terek nagyon széles tartományának alapcsoportját.

Ez a tétel azt mondja, hogy ha X két alterülete , mindkettő nyitva, vagy mindkettő zárt, tartalmaz egy x pontot, és ívekkel összekötött metszéspontja van, akkor az x-re mutató két tér egyesülésének alapvető csoportja az összevont összeg (az csoportok) az alapcsoportokból a két tér x-be , az összevonás kereszteződésük alapvető csoportja mentén történik.

π1(V1∪V2,x)=π1(V1,x)⋆π1(V1∩V2,x)π1(V2,x).{\ displaystyle \ pi _ {1} (V_ {1} \ csésze V_ {2}, x) = \ pi _ {1} (V_ {1}, x) {\ alulhúzás {\ pi _ {1} (V_ {1} \ cap V_ {2}, x)} {\ star}} \ pi _ {1} (V_ {2}, x).}

Kúptétel és a projektív terek alapvető csoportja

Meghatározzuk az X topológiai tér kúpját mint hányados teret

VSx=(x×én)/(x×{0}){\ displaystyle CX = (X \ alkalommal I) / (X \ alkalommal \ {0 \}) \,}

A termék a X-szerese az egységnyi intervallumot I = [0, 1].

(Ha X kör, akkor egy forradalmi kúp részét kapjuk .)

Bármely C ( X ) kúp egyszerűen összekapcsolódik (mert összehúzható).

Van kanonikus zárványunk X = X × {1} ⊂ C ( X ).

Ha f  : X → Y folyamatos térkép két topologikus terek, definiáljuk a kúp C ( f ) a térkép F hányadosaként diszjunkt Unió C ( X ) ⊔ Y az azonosító minden egyes eleme X az X ⊂ C ( X ) az f ( x ) képpel Y-ben .

Példák  : ha f a 2. fok térképe a körben: S 1 → S 1 , z ↦ z 2 , akkor megkapjuk a C ( f ) = P 2 (ℝ) értéket, a valódi projektív síkot . Általánosabban, az n ≥ 1, ha f a kanonikus vetülete a gömb S n -1 -ra a valós projektív teret P n -1 (ℝ), C ( F ) = P n (ℝ).

A kúp-tétel kimondja, hogy ha X van csatlakoztatva ívek, az alapvető csoport C ( F ) izomorf a hányadosa π 1 ( Y ) a normalizált  (en) alcsoport π 1 ( Y ) kép f ✻ .

Alkalmazás  : az n ≥ 2 esetén a P n (ℝ) projektív tereknek alapvető csoportjai vannak izomorfak a ℤ / 2ℤ-vel.

Grafikonok, felületek és poliéderek alapvető csoportja

• Az összekapcsolt gráf alapvető csoportja egy szabad csoport (lásd Nielsen-Schreier-tétel ).
• A poliéder alapvető csoportja elismeri a generátorok és a relációk bemutatását , a kapcsolatot a poliéder mindkét oldala biztosítja.
• Az alapvető csoportja egy orientálható kompakt felülete a nemzetség g elismeri a prezentáció 2 g generátorok egy 1 , b 1 , ..., a g , b g és csak egy kapcsolatban [ a 1 , b 1 ] ... [ a g , b g ] = 1 (választható a prezentáció a 1 … a g b 1 … b g a 1 −1 … a g −1 b 1 −1 … b g −1 = 1).

Csomóelmélet

A csomópontelméletben megpróbáljuk megkülönböztetni a nem izotópos csomópontokat . Az alapvető csoportja a komplement egy csomópont ad invariáns csomópontok , amely lehetővé teszi, hogy különbséget néhány közülük.

Általánosítások

Fundamentális groupoid (vagy Poincaré groupoid)

A kategóriát akkor nevezzük csoportoidnak, ha az objektumok és a nyilak halmazt alkotnak (ez egy kis kategória ), és ha az összes nyil megfordítható (izomorfizmus). A csoportoidok olyan kategóriát alkotnak, amelynek morfizmusai a csoportoidok közötti függvények. A csoportok csoportok (egyetlen objektummal).

Legyen G groupoid, akkor definiáljuk az x ≡ y ekvivalencia relációt, ha az x- től y- ig terjedő morfizmusok G ( x , y ) halmaza nem üres. A hányadoshalmazt (amelynek objektumai az ekvivalenciaosztályok) π 0 ( G ) -vel jelöljük . Ha f a csoportoidok morfizmusa, akkor f kompatibilis a ≡ ekvivalencia relációval. A hányadossal való áthaladással a π 0 meghatároz egy functort ( a csatlakoztatott komponensek functorját ) a groupoidok kategóriájától a halmazok kategóriájáig.

Hadd G egy groupoid, és x tárgya G (mi is mondjuk pont a G ). A G ( x , x ) nyilai közötti összetétel törvénye, amely erre az alcsoportra korlátozódik, csoporttörvény. Ezt a csoportot π 1 ( G , x ) -vel jelöljük . Megjegyzés: A π 1 nem határoz meg egy functort a groupoidok kategóriájától a csoportok kategóriájáig.

Minden topológiás X teret összekapcsolunk olyan funkcióval egy csoportoid π X  : az összes objektumot π X az összes mögöttes X-nek vesszük . Az x forrás és az y cél nyilai az x- től y- ig terjedő utak (= folytonos ívek) homotópiás osztályai . A homotópiai viszony kompatibilis az utak összetételével, és így meghatározza az π X csoportot, amelyet X fundamentális csoportjának nevezünk . A van Kampen-tételt egyszerűen csak az alapvető csoportoidok használatával fejezzük ki.

Az alapcsoportot az határozza meg

π1(x,x0)=π1(πx,x0).{\ displaystyle \ pi _ {1} (X, x_ {0}) = \ pi _ {1} (\ pi X, x_ {0}).}

Az alapcsoport valójában az első homotópiacsoport , ezért az π 1 ( X ) jelölés indexe 1 .

Alapcsoport és algebrai geometria

Az X tér burkelméletében definiáljuk az π E  : E → X burkolat rostját a p pontban, mint a π E −1 ( p ) halmazot, amelyet szintén E ( p ) jelöl . Az E ↦ E ( p ) levelezés meghatározza az alapburkolatok ( X , p ) kategóriájának funkcióját a halmazok kategóriájában. Az alapcsoport elvont módon definiálható a szálfunkciós automorfizmusok csoportjaként , amely egy alap burkolattal ( X , p ) társítja az E ( p ) -t .

Ez az alternatív definíció megnyitja az utat az általánosításhoz az algebrai geometriában , ahol a korábban megadott p alapfűzőkre vonatkozó definíció természetesen nem érvényes. Ebben az általánosításban a burkolatokat étale-morfizmusok váltják fel: a hegyes tér ( X , p ) alapvető csoportja a szálfaktor automorfizmusainak csoportja, amely egy étális morfizmussal E → X társítja az E ( p ) rostot . pontban p . Ezt az általánosítást Alexandre Grothendieck és Claude Chevalley köszönheti .

Ez az elmélet lehetővé teszi, hogy ismertesse a kapcsolatot a Galois elmélet burkolatok Riemann felületek (csoport automorfizmusok ...), és a Galois-elmélet funkció területeken .

Megjegyzések és hivatkozások

1. Pierre Dolbeault , komplex vizsgálata , Masson,1990, P.  120.
2. (a) J. Dieudonné , története algebrai és differenciál topológia, 1900-1960 , p.  17–24.
3. Jean Lannes , „  Alapvető csoport  ” ( Archívum • Wikiwix • Archive.is • Google • Mit kell tenni? ) , École Polytechnique,2006.
4. Claude Godbillon , Az algebrai topológia elemei [ a kiadás részlete ], P.  68-69 .
5. Godbillon , p.  83.
6. Régine és Adrien Douady , Algebra és Galois elméletek [ a kiadások részletei ], 2 -én ed., Cassini, 2005, p.  265 .
7. Jean Dieudonné , Az elemzés elemei , vol.  3, Bordas,1974, P.  196.
8. André Gramain , Felületek topológiája , PUF ,1971, P.  10..
9. Godbillon , p.  71.
10. Dolbeault 1990 , p.  103 és 120.
11. R. és A. Douady , p.  266.
12. Michel Zisman , Elemi algebrai topológia , Armand Colin,1972, P.  49.
13. Gramain 1971 , p.  15.
14. (en) Allen Hatcher , algebrai topológia , CUP ,2001( ISBN  978-0-521-79540-1 , online olvasás ) , p.  291.
15. Godbillon , p.  76.
16. Lannes 2006 ihlette . A lényeg lényegének egyszerűbb bizonyítását lásd a " Bearing tétel  " cikkben  .
17. Lásd még: „  Eilenberg-MacLane Space  ”.
18. R. és A. Douady , p.  237.
19. R. és A. Douady , p.  218.
20. Lannes 2006 , p.  12.
21. H. Cartan , Cours de C3, Algebra és geometria: Alapcsoport, bevonatok , Orsay, 1968-1969 ( olvasható online ) , p.  8..
22. Zisman 1972 , p.  91.

Külső hivatkozás

Az alapvető csoportot bemutató animációk, Nicolas Delanoue

<img src="https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">