A fraktálok listája Hausdorff dimenzió szerint

Ez a cikk a fraktálok listája, Hausdorff dimenzió növelésével rendezve .

A matematikában a fraktál olyan metrikus tér, amelynek Hausdorff-dimenziója (megjegyezve δ) szigorúan nagyobb, mint a topológiai dimenzió . Legalábbis ezt a meghatározást eredetileg Benoît Mandelbrot adta meg , de gyorsan felváltotta egy homályosabb meghatározással , lehetővé téve például a Hilbert-görbe beillesztését .

Determinisztikus fraktálok

δ <1

δ (pontos érték)	δ (hozzávetőleges val.)	Vezetéknév	Megjegyzések
0 ⇒ tehát nem fraktál, hanem homályos boxszámlálás = 1	0	Racionális számok	A megszámlálható halmazok Hausdorff-dimenziója mindig nulla. Ezek a halmazok nem lehetnek fraktálok. Tegyük hozzá, hogy egy ilyen halmaz "dobozszámlálás" dimenziója eltérő lehet, ha ez egy R nyitott régiójának sűrű részhalmaza. A racionális számok halmazának "1" dobozszámlálási dimenziója van, mert a bezárása R.
Számított	0,538	Feigenbaum attraktor	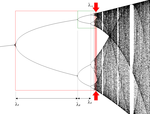A Feigenbaum attraktor (a nyilak között) az a pontkészlet, amelyet a kritikus paraméter logisztikai függvényének egymást követő iterációi hoznak létre , ahol a periódusok megduplázódása végtelen. Megjegyzés: ez a dimenzió megkülönböztethető és unimodális funkció esetén megegyezik. ${\ displaystyle \ lambda _ {\ infty} = 3 {,} 570}$
${\ displaystyle {\ frac {\ log 2} {\ log 3}}}$	0,6309	Cantor szettje	Úgy épült, hogy minden iterációnál eltávolította a középső harmadot. Sehol sűrű és nulla mértékű, de megszámlálhatatlan . Általánosítás : Az általánosított Cantor-készlet úgy épül fel, hogy az egyes szegmenseknél és az $n-$ edik iterációnál eltávolítja a hosszúság központi szegmensét . Fraktáldimenziója akkor megéri, és minden értéket 0 és 1 közé vehet. A szokásos Cantor-halmaz épül fel . ${\ displaystyle \ gamma ^ {n}}$ ${\ displaystyle - {\ frac {1} {\ log _ {2} {\ frac {1- \ gamma} {2}}}}}$ ${\ displaystyle \ gamma = 1/3}$
${\ displaystyle \ log _ {2} \ varphi}$	0,6942	Aszimmetrikus Cantor készlet	Figyelje meg, hogy a dimenzió már nem , vagy akár (a fenti szimmetrikus eset ). A második negyed minden egyes iterációval történő eltávolításával épült. Sehol sűrű és nulla mértékű, de megszámlálhatatlan . ${\ displaystyle {\ frac {1} {\ log _ {2} 3}}}$ ${\ displaystyle {\ frac {1} {3- \ log _ {2} 3}}}$ ${\ displaystyle \ gamma = {\ tfrac {1} {4}}}$ ${\ displaystyle \ varphi = (1 + {\ sqrt {5}}) / 2}$ ( aranyarány ).
${\ displaystyle {\ frac {\ log (5)} {\ log (10)}}}$	0.69897	Valós számok tizedesjegyekkel	Felidézve a Cantor halmazát .
${\ displaystyle {\ frac {\ log (5)} {\ log (9)}}}$	0,7325	UNU fraktál	A következő diagram egymást követő iterációival konstruált önleíró fraktál: u → unu (a „u”) → unuunnunu (a „u”, „n”, „u”) → stb.

1 ≤ δ <2

δ (pontos érték)	δ (hozzávetőleges val.)	Vezetéknév	Rajz	Megjegyzések
$1$	1.0000	Smith-Volterra-Cantor együttes		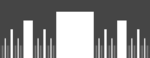Beépített eltávolításával a negyedik és a tizenhatodik, a 64 th ... központi minden iterációban. Sehol sem sűrű, de megszámlálhatatlan, és Lebesgue mércéje 1/2. Ennek tehát 1. dimenziója van.
${\ displaystyle 2+ \ log _ {2} (1/2) = 1}$	1.0000	Takagi vagy Blancmange görbe		Állítsa be az egység intervallumra , ahol van a "fűrészfog" funkció. Speciális eset a Takahi-Landsberg görbe: a . A Hausdorff dimenzió érvényes . ${\ displaystyle f (x) = \ sum _ {n = 0} ^ {\ infty} {s (2 ^ {n} x) \ felett 2 ^ {n}}}$ $s (x)$ ${\ displaystyle f (x) = \ sum _ {n = 0} ^ {\ infty} {w ^ {n} s (2 ^ {n} x)}}$ ${\ displaystyle w = 1/2}$ ${\ displaystyle 2+ \ log _ {2} w}$
számított	1.0812	Julia beállította a z² + 1/4-et		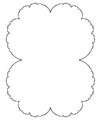Julia beállította a c = 1/4 értéket.
Megoldás s az $2 \| \ alpha \| ^ {{3s}} + \| \ alpha \| ^ {{4s}} = 1$	1.0933	Rauzy Fractal Boundary	$Rauzy fractal.png$	Geometriai ábrázolása dinamikus rendszer kapcsolódó szubsztitúciós Tribonacci: , és . a konjugált komplex gyökerek egyike . ${\ displaystyle 1 \ mapsto 12}$ ${\ displaystyle 2 \ mapsto 13}$ ${\ displaystyle 3 \ mapsto 1}$ $\ alfa$ $z ^ {3} -z ^ {2} -z-1 = 0$
${\ displaystyle 2 {\ frac {\ log (3)} {\ log (7)}}}$	1.12915	Gosper-sziget		Mandelbrot (1977) nevezte el. A Gosper-görbe határa .
Mért ( dobozszámlálás )	1.2	Julia beállította a c = i értéket (dendrit)		Julia beállította a c = i értéket
${\ displaystyle 3 {\ frac {\ log (\ varphi)} {\ log \ left ({\ frac {3 + {\ sqrt {13}}} {2}} \ right)}}}$	1.2083	Fraktál a Fibonacci szó a 60 °		A Fibonacci szóból épült , 60 ° -os szöggel. Lásd még az alábbiakban a standard Fibonacci szó fraktálját. With ( arany arány ). ${\ displaystyle \ varphi = (1 + {\ sqrt {5}}) / 2}$
	1.2107	Twindragon szelíd határ		Az egyik a hat szokásos 2 autóból (egyforma nagyságú, két saját példányból is kikövezhető ).
${\ displaystyle {\ frac {\ log (3)} {\ log (1 + {\ sqrt {2}})}}}$	1.2465	Fibonacci szó fraktál átnyúló		A Fibonacci szóból épült . Lásd még az alábbiakban a szokásos Fibonacci szó fraktálját. With ( arany arány ). ${\ displaystyle \ varphi = (1 + {\ sqrt {5}}) / 2}$
	1.26	Hénon attraktor		A kanonikus Henon-térkép ( a = 1,4 és b = 0,3) δ = 1,261 ± 0,003. Különböző paraméterek különböző δ értékekhez vezetnek.
${\ displaystyle \ log _ {3} 4}$	1.2619	Koch görbe		Ha ezt a háromszöggörbét háromszor egymás mellé helyezzük, akkor megkapjuk a Koch-pehelyt és az anti-Koch-pehelyt, ha az megfordul.
${\ displaystyle \ log _ {3} 4}$	1.2619	Terdragon görbe határ		L-rendszer : hasonló a sárkány görbéhez 30 ° -os szöggel. A Fudgeflake úgy van megépítve, hogy három kezdő szegmenst háromszögben egymás mellé állít .
${\ displaystyle \ log _ {3} 4}$	1.2619	Kántor tér		Kétdimenziós Cantor készlet .
számított	1.2683	Julia beállította a z ²-1 értéket		Julia beállította a c = -1 értéket.
Mért (dobozszámlálás)	1.3	Beryl fraktál k = 1 esetén	$Beryl fractal.png$	K = 1 esetén. A Beryl fraktál határozza meg a komplex x és y , c egy pontot a komplex síkban, és a vágás a síkban ${\ displaystyle x_ {0} = c ~, ~ y_ {0} = 1 ~; ~ x_ {n + 1} = k (x + y) ~, ~ y_ {n + 1} = xy-y ^ {2 }}$ $\ nu _ {0} = 1$
számított	1.3057	Apollóniusz Baderne		Lát
számított (dobozszámlálás)	1.328	5 körös inverziós fraktál		A beállított határérték 5 érintő körhöz képest inverziók révén iteratív módon generálódott. Apollonius jelvénye is, 4 alapkörrel. Lát
számított	1.3934	Douady nyúl		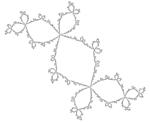Julia beállította a c = -0,123 + 0,745i értéket.
Mért (dobozszámlálás)	1,42 ± 0,02	Newton fraktálja	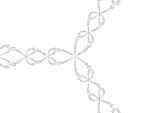$Newton fractal.png$	Hármas határ a vonzás medencék a 3 komplex gyökerei az egyenlet által Newton-módszerrel . $z ^ {3} -1 = 0$
${\ displaystyle \ log _ {3} 5}$	1.4649	Vicsek fraktál	$Box fractal.svg$	Úgy épül fel, hogy minden négyzetet iteratív módon 5 négyzet alakú kereszttel helyettesítünk.
${\ displaystyle \ log _ {3} 5}$	1.4649	Másodfokú Koch-görbe (1. típus)		Azt látjuk, hogy a minta a fraktál doboz (lásd fent), épített másképp.
${\ displaystyle \ log _ {4} 8 = {\ frac {3} {2}}}$	1,5000	Másodfokú Koch-görbe (2. típus)		Más néven „Minkowski kolbász”.
${\ displaystyle 2- \ log _ {2} {\ sqrt {2}} = {\ frac {3} {2}}}$ (helyesen feltételezett)	1,5000	a Weierstrass funkció : 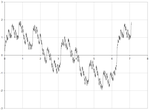${\ displaystyle f (x) = \ sum _ {k = 1} ^ {\ infty} {\ frac {\ sin (2 ^ {k} x)} {{\ sqrt {2}} ^ {k}}} }$		A Weierstrass függvény Hausdorff dimenziója, amelyet a és határol, határozza meg . Sejtik, hogy ez a pontos érték. Ugyanez az eredmény megállapítható a szinuszfüggvény helyett más periodikus függvények, például a koszinusz használatával. ${\ displaystyle f: [0,1] \ - \ mathbb {R}}$ ${\ displaystyle f (x) = \ sum _ {k = 1} ^ {\ infty} {\ frac {\ sin (b ^ {k} x)} {a ^ {k}}}}$ $1 <a <2$ $b> 1$ ${\ displaystyle 2- \ log (a) / \ log (b).}$
${\ displaystyle \ log _ {2} {\ frac {1 + {\ sqrt [{3}] {73-6 {\ sqrt {87}}}} + {\ sqrt [{3}] {73 + 6 { \ sqrt {87}}}}} {3}}}$	1.5236	Sárkány ívelt szegély		Lásd: Chang & Zhang.
${\ displaystyle \ log _ {2} {\ frac {1 + {\ sqrt [{3}] {73-6 {\ sqrt {87}}}} + {\ sqrt [{3}] {73 + 6 { \ sqrt {87}}}}} {3}}}$	1.5236	Twindragon határ		Az egyik a hat szokásos 2 autóból (egyforma nagyságú, két saját példányból is kikövezhető ).
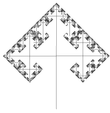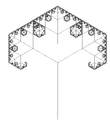
${\ displaystyle \ log _ {2} 3}$	1.5849	Három ágú fa		Minden ágnak három ága van (itt 90 ° és 60 °). A fa fraktál dimenziója a terminális ágaké.
${\ displaystyle \ log _ {2} 3}$	1.5849	Sierpiński háromszög		Ez Pascal háromszöge modulo 2 is.
${\ displaystyle \ log _ {2} 3}$	1.5849	Arrowhead Sierpiński görbe		Ugyanaz a határ, mint a Sierpiński-háromszög (fent), de egydimenziós görbe iterációjával kapott.
${\ displaystyle \ log _ {2} 3}$	1.5849	Border a fraktál a konzol (en) (T-square)
${\ displaystyle {\ frac {\ log \ varphi} {\ log {\ sqrt [{\ varphi}] {\ varphi}}}}}$	1,61803 = $\ varphi$	egy arany sárkány		Beépített két arány méretezés és , ahol . A dimenzió azért ér, mert . With ( arany arány ). $r$ $r ^ {2}$ ${\ displaystyle r = 1 / \ varphi ^ {1 / \ varphi}}$ $\ varphi$ ${\ displaystyle ({r ^ {2}}) ^ {\ varphi} + r ^ {\ varphi} = 1}$ ${\ displaystyle \ varphi = (1 + {\ sqrt {5}}) / 2}$
$1+ \ log _ {3} (2)$	1.6309	Pascal háromszöge modulo 3		Általánosságban elmondható, hogy egy modulo k háromszög esetében, ha k elsődleges, a fraktál mérete (vö. Stephen Wolfram) ${\ displaystyle 1+ \ log _ {k} {\ frac {k + 1} {2}}}$
${\ displaystyle \ log _ {3} 6}$	1.6309	Sierpinski hatszög		A Sierpinski szőnyeg módjára épült, hatszögletű hálózaton, 6 hasonlóság 1/3 arányban. Észrevesszük a Koch hópehely mindenütt jelenlétét .
${\ displaystyle 3 {\ frac {\ log \ varphi} {\ log (1 + {\ sqrt {2}})}}}$	1.6379	Fibonacci fraktál		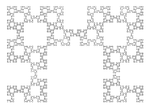Fraktál a Fibonacci szó (vagy nyúlszekvencia) alapján Sloane A005614. Illusztráció: Fraktál az F 23 = 28657 szegmens után. With ( Arany arány ). ${\ displaystyle \ varphi = (1 + {\ sqrt {5}}) / 2}$
Megoldása ${\ displaystyle (1/3) ^ {s} + (1/2) ^ {s} + (2/3) ^ {s} = 1}$	1.6402	Olyan IFS vonzereje, amelynek három hasonlósága van: 1/3, 1/2 és 2/3		Általánosítás: Feltételezve, hogy a feltétele egész elégedett, vonzod a funkció rendszer végigjárt a simulitudes arány , a halmaz , egyenlet megoldása: . $nem$ $c_ {n}$ $s$ ${\ displaystyle \ sum _ {k = 1} ^ {n} c_ {k} ^ {s} = 1}$
$1+ \ log _ {5} (3)$	1.6826	Pascal háromszöge modulo 5		Általánosságban elmondható, hogy egy modulo k háromszög esetében, ha k elsődleges, a fraktál mérete (vö. Stephen Wolfram) ${\ displaystyle 1+ \ log _ {k} {\ frac {k + 1} {2}}}$
Mért (dobozszámlálás)	1.7	Ikeda Attractor		Az a = 1, b = 0,9, k = 0,4 és p = 6 paraméterértékekhez az Ikeda iterált rendszerben . Származéka síkhullámok kölcsönhatásainak modellezéséhez lézerben. Különböző paraméterek különböző értékeket eredményeznek. ${\ displaystyle z_ {n + 1} = a + bz_ {n} \ exp [i [kp / (1+ \ lfloor z_ {n} \ rfloor ^ {2})]]}$
${\ displaystyle {\ frac {\ log 4} {\ log {\ sqrt {5}}}}}$	1.7227	Szélkerék fraktál		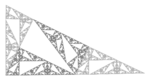Épült az útburkoló szélmalom a John Conway .
${\ displaystyle \ log _ {3} 7}$	1.7712	Sierpinski hatszög		Úgy épül fel, hogy minden hatszöget 7-es hatszög-pelyhel helyettesítünk. Határa a Koch hópehely. Végtelen Koch-pelyhet tartalmaz (pozitív és negatív).
napló (7) / napló (3)	1.7712	Rivera Fractal HI		Kezdve egy négyzettel, amely a méreteit három egyenlő részre osztja, és így az első négyzettel kilenc önhasonló négyzetet alkot, két középső négyzetet (a fenti és a központi négyzet alatti négyzetet) törölnek mind a hét meg nem szüntetett négyzetből. a folyamat megismétlődik, így a végtelenségig folytatódik.
${\ displaystyle {\ frac {\ log 4} {\ log (2 (1+ \ cos (85 ^ {\ circ}))}}}$	1.7848	85 ° Koch görbe, Cesàro fraktál		Általánosítása a Koch-görbe alapján szögben van választjuk között 0 és 90 °. A fraktál dimenzió ekkor érvényes . Cesàro fraktálja erre a motívumra épül. ${\ displaystyle {\ frac {\ log N} {\ log (2 \ bal (1+ \ cos a) \ jobb)}}}$
${\ displaystyle \ log _ {2} (3 ^ {0 {,} 63} + 2 ^ {0 {,} 63})}$	1,8272	Önfinomító fraktál		Iteratív módon épült a négyzet alakú rácsból , a . Hausdorff dimenziója megegyezik a k oszlop elemeinek számával és számával. A Minkowski - Bouligand dimenzió ( dobozszámlálás ) más képletet ad, ezért gyakran más értéket. Az önhasonló fraktálokkal ellentétben az ön-affinális fraktálok Hausdorff-dimenziója az iterált elemek helyzetétől függ, és az általános esetre nincs egyszerű képlet. $p \ szer q$ ${\ displaystyle p \ leq q}$ ${\ displaystyle \ log _ {p} \ balra (\ sum _ {k = 1} ^ {p} n_ {k} ^ {a} \ jobbra)}$ ${\ displaystyle a = {\ frac {\ log p} {\ log q}}}$ $n_k$
${\ displaystyle {\ frac {\ log (6)} {\ log (1+ \ phi)}}}$	1.8617	Flake ötszögű (en) ( pentaflake)		Úgy épül fel, hogy minden ötszöget iteratív módon 6 ötszögnyi pelyhekkel helyettesítünk. Itt van az aranyarány, és érdemes $\ phi$ ${\ displaystyle (1 + {\ sqrt {5}}) / 2}$
oldata ${\ displaystyle 6 (1/3) ^ {s} +5 {(1/3 {\ sqrt {3}})} ^ {s} = 1}$	1.8687	A "majomfa"		Ez a görbe ezen a néven jelenik meg ( Mandelbrot 1982 ). Ennek alapja az $1/3$ arány 6 dilatációja és az arány 5 dilatációja . ${\ displaystyle 1 / (3 {\ sqrt {3}})}$
${\ displaystyle \ log _ {3} 8}$	1.8928	Sierpiński szőnyeg
${\ displaystyle \ log _ {3} 8}$	1.8928	Kántor kocka		Háromdimenziós Cantor készlet .
${\ displaystyle \ log _ {3} 4+ \ log _ {3} 2 = \ log _ {3} 8}$	1.8928	A von Koch-görbe és a Cantor-készlet derékszögű szorzata		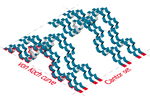Általánosítás: Legyen F × G két F és G fraktálkészlet derékszögű szorzata. Ezután $tompítsa H (F \times G) = dim H (F) + dim H (G)$ .
Értékelve	1.9340	Lévy fraktál határ		Becslések: Duvall és Keesling (1999). Maga a Lévy fraktál Hausdorff 2. dimenzióval rendelkezik.
	1,974	Penrose kövezés		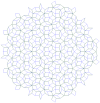Lásd: Ramachandrarao, Sinha és Sanyal

δ = 2

δ (pontos érték)	δ (hozzávetőleges val.)	Vezetéknév	Rajz	Megjegyzések
$2$	2	Mandelbrot beállította a határt		A határ ugyanolyan dimenzióval rendelkezik, mint az egész.
$2$	2	néhány julia készlet		A c meghatározott értékeire (a Mandelbrot halmaz határán) a Julia halmaznak van 2 dimenziója.
$2$	2	Sierpiński görbe (be)		Bármely görbe kitöltési tér Hausdorff dimenzióval rendelkezik δ = 2.
$2$	2	Hilbert görbe		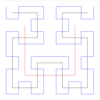Három dimenzióra bővíthető.
$2$	2	Peano görbe		és hasonló építési görbékből álló család, ideértve a Wunderlich görbéket is .
$2$	2	Curve Moore (en)		3 méretre bővíthető.
$2$	2	Lebesgue görbe		A fenti görbéktől eltérően ez szinte mindenhol megkülönböztethető . A 2D görbe második típusát is meghatározták. Ez a görbe 3D-ben meghosszabbítható, 3 fraktál dimenzióval.
${\ displaystyle {\ frac {\ log 2} {\ log {\ sqrt {2}}}}}$	2	Sárkány görbe		Határának fraktálmérete 1,5236 (lásd Chang & Zhang)
	2	"Terdragon" görbe		L-rendszer : F → F + FF; szög = 120 °.
${\ displaystyle \ log _ {2} 4}$	2	Peano-Gosper görbe		A kerete Gosper Island .
Megoldása ${\ displaystyle 7 ({1/3}) ^ {s} +6 ({1/3 {\ sqrt {3}}}) ^ {s} = 1}$	2	Görbe kitöltve a Koch hópelyhet		Mandelbrot javasolta 1982-ben, és kitölti a Koch hópelyhét . 7 1/3-os és 6-os hasonlóságon alapul . ${\ displaystyle 1/3 {\ sqrt {3}}}$
${\ displaystyle \ log _ {2} 4}$	2	Sierpinski tetraéderje		A 2. dimenzió következtében a felülete az iterációtól az iterációig változatlan marad, egészen a végtelenig.
${\ displaystyle \ log _ {2} 4}$	2	Fractal H (in)	$H fractal2.png$	Továbbá a Mandelbrot fa, amelynek hasonló szerkezete van.
${\ displaystyle {\ frac {\ log (1/2)} {\ log (1 / {\ sqrt {2}})}}}$	2	Pitagoraszi fa		Mindegyik négyzet két oldal négyzetet generál, amelyet 1 / gyökérrel csökkentett (2).
${\ displaystyle \ log _ {2} 4}$	2	Görög keresztfraktál		Mindegyik szegmenst négy szegmens alkotja.

2 <δ <3

δ (pontos érték)	δ (hozzávetőleges val.)	Vezetéknév	Rajz	Megjegyzések
Mért	2,01 + -0,01	Rössler attraktor		A Rössler-attraktor fraktálmérete valamivel nagyobb, mint 2. A = 0,1, b = 0,1 és c = 14 esetén a becslések szerint 2,01 és 2,02 között van.
Mért	2,06 + -0,01	Lorenz furcsa vonzereje		Az attraktor paraméterei: v = 40, = 16 és b = 4. $\ sigma$
${\ displaystyle \ log _ {2} 5}$	2.3219	Fraktál piramis		Mindegyik piramist 5 piramis váltja fel. Nem szabad összetéveszteni Sierpinski tetraéderével, ezek négyzet alapú piramisok.
${\ displaystyle {\ frac {\ log (20)} {\ log (2+ \ phi)}}}$	2.3296	Fraktál dodekaéder	$Dodecaedron fractal.jpg$	Minden dodekaédert 20 dodekaéder helyettesít.
${\ displaystyle \ log _ {3} (13)}$	2.33	1. típusú háromdimenziós kvadratikus Koch felület		Az 1. típusú kétdimenziós Koch másodfokú görbe háromdimenziós kiterjesztése (az ábra a második iterációt szemlélteti).
	2.47	Hézagai a szférák Apollonius		Apolloniusi Baderne három dimenzióban. Modellezze a zsemlemorzsát vagy a szivacsot. A méretet M. Borkovec, W. De Paris és R. Peikert számította.
${\ displaystyle \ log _ {4} (32)}$	2.50	2. típusú háromdimenziós kvadratikus Koch felület		A 2-es típusú kétdimenziós Koch másodfokú görbe háromdimenziós kiterjesztése (az ábra a második iterációt szemlélteti).
${\ displaystyle \ log _ {3} (16)}$	2.5237	Cantor Hypercube	képviselet nem lehetséges	Cantor 4 dimenzióban. Általánosságban elmondható, hogy az n dimenziós térben a Cantor halmaz fraktál dimenziója egyenlő ${\ displaystyle \ log _ {3} 2}$
${\ displaystyle {\ frac {\ log ({\ frac {\ sqrt {7}} {6}} - {\ frac {1} {3}})} {\ log ({\ sqrt {2}} - 1 )}}}$	2,529	Jeruzsálem kocka		Homotetikus aránya irracionális, érdemes . Az n kockán lévő iteráció nyolc kockát alkot a következő n + 1 rangú és tizenkét kockát n + 2 rangú. Összehasonlítva a Menger szivaccsal , amelynek térfogata szintén nulla. ${\ displaystyle {\ sqrt {2}} - 1}$
${\ displaystyle {\ frac {\ log (12)} {\ log (1+ \ phi)}}}$	2.5819	Fractal Icosahedron	$Icosaedron fractal.jpg$	Minden ikozaéder helyébe 12 ikozaéder lép.
${\ displaystyle \ log _ {2} 6}$	2.5849	Fraktál oktaéder	$Octaedron fractal.jpg$	Mindegyik oktaéder helyébe 6 oktaéder lép.
${\ displaystyle \ log _ {2} 6}$	2.5849	Koch felület		Minden egyenlő oldalú háromszöget 6 kétszer kisebb háromszög helyettesít. A Koch-görbe kétdimenziós kiterjesztése .
${\ displaystyle \ log _ {2} 6}$	2.59	Háromdimenziós görög keresztfraktál		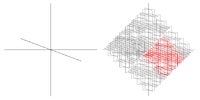Mindegyik szegmenst három szegmensből álló háromdimenziós kereszt váltja fel. A kétdimenziós kereszt háromdimenziós kiterjesztése.
${\ displaystyle {\ frac {\ log (3)} {\ log (3/2)}}}$	2.7095	Von Koch 3D-ben (Delta Fractal)		A 6 egyenlő szárú sokszögnek olyan része van, amelynek oldalai 2: 2: 3 arányúak. cserélje ki az egyes poliédereket, nem pedig három példányt, 2/3-mal kisebbet.
${\ displaystyle \ log _ {3} (20)}$	2.7268	Menger szivacs		A felület egy fraktáldimenziója . ${\ displaystyle \ log _ {3} (12) \ kb 2 {,} 2618}$
${\ displaystyle \ log _ {2} 7}$	2.8073	Fraktál- heptaéder		7 1/2 arányú méretezéssel épült. Arcai Sierpinski háromszögekből állnak. Térfogata a nulla felé hajlik.

δ = 3

δ (pontos érték)	δ (hozzávetőleges val.)	Vezetéknév	Megjegyzések
${\ displaystyle \ log _ {2} 8}$	3	Háromdimenziós Hilbert-görbe	Hilbert görbe három dimenzióra terjedt ki
${\ displaystyle \ log _ {2} 8}$	3	Háromdimenziós Lebesgue görbe	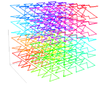A Lebesgue-görbe három dimenzióra terjedt ki
${\ displaystyle \ log _ {2} 8}$	3	Görbe Moore (in) háromdimenziós	Moore görbe három dimenzióra terjedt ki.
$3$	3	Mandelbulb	A Mandelbrot készlet (8. teljesítmény) kiterjesztése 3 dimenzióra.

Véletlenszerű és természetes fraktálok

δ (pontos érték)	δ (hozzávetőleges val.)	Vezetéknév	Megjegyzések
1/2	0.5	A Brown-függvény grafikonjának nulla ( Wiener-folyamat )	A Brown-függvény grafikonjának nullái sehol sem sűrű halmazat alkotnak , a Lebesgue-féle 0-s mértékű fraktálszerkezettel.
Megoldás a és $E (C_ {1} ^ {s} + C_ {2} ^ {s}) = 1$ $E (C_ {1}) = 0,5$ $E (C_ {2}) = 0,3$	0,7499	Véletlenszerű kantárkészlet 50% / 30%	Minden iterációnál a bal intervallum hosszát egy véletlen változó határozza meg : az eredeti szegmens hosszának változó százaléka. Ugyanez a jobb oldali intervallumra, egy másik véletlen változóval . Hausdorff dimenziója kielégítette az egyenletet . ( A matematikai elvárás a ). $C_1$ $C_2$ $s$ $E (C_ {1} ^ {s} + C_ {2} ^ {s}) = 1$ $VOLT)$ $x$
Mért	1.05	Humán kromoszóma n o 22	A számítási módszer részleteit lásd a referenciában.
Megoldása $s + 1 = 12 * 2 ^ {{- (s + 1)}} - 6 * 3 ^ {{- (s + 1)}}$	1,144…	Koch görbe véletlenszerű intervallummal	A medián intervallum hossza egyenletesen eloszlott véletlen változó (0; 1/3).
Mért	1.24	Nagy-Britannia partjai	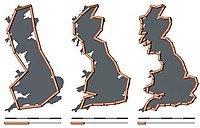Nagy-Britannia nyugati partjának fraktáldimenziója, Lewis Fry Richardson által mérve és Benoît Mandelbrot idézi .
${\ displaystyle \ log _ {3} 4}$	1.2619	Koch görbe véletlenszerű orientációval	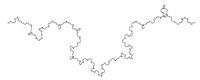Bemutatunk itt egy olyan véletlenszerű elemet, amely nem befolyásolja a dimenziót, ha véletlenszerűen választjuk az egyes iterációknál az egyenlő oldalú háromszöget a görbe fölé vagy alá.
${\ frac 43}$	1.33	Brown-mozgás határ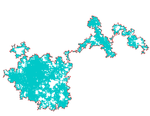
${\ frac 43}$	1.33	Kétdimenziós polimer	Hasonló a metszés nélküli Brown-mozgáshoz.
${\ frac 43}$	1.33	Elülső perkoláció , elülső korrózió kétdimenziós	A perkolációs front fraktál dimenziója invázióval a perkolációs küszöbön (59,3%). Ez egyben a korróziós front fraktálmérete is.
	1.40	Az aggregátumok összesítése két dimenzióban	Az aggregátumok fokozatosan egyetlen 1,4 dimenziós aggregátumgá egyesülnek.
${\ displaystyle 2 - {\ frac {1} {2}}}$	1.5	A Brown- függvény grafikonja ( Wiener-folyamat )	Olyan függvény grafikonja, amely bármely pozitív valós pár esetén és képük különbsége a Gauss-féle varianciaeloszlás középpontját követi . Általánosítás: Az index egy tört Brown-függvénye ugyanazt a meghatározást követi, de varianciával = , ebben az esetben a grafikon Hausdorff-dimenziója = . $f$ $x$ $x + h$ $f (x + h) -f (x)$ $h$ $\ alfa$ $h ^ {{2 \ alpha}}$ $2- \ alfa$
Mért	1.52	Norvég tengerpart	Lásd Feder.
Mért	1.55	Véletlenszerű séta kereszteződés nélkül	Véletlenszerű séta négyzet alakú hálózaton önmetszés nélkül, visszaváltási algoritmussal a holtpontok elkerülése érdekében.
${\ displaystyle {\ frac {5} {3}}}$	1.66	Háromdimenziós polimer	Hasonló a köbös rácsos Brown-mozgáshoz, de önmetszés nélkül.
	1.70	Kétdimenziós diffúziós aggregátum	Két dimenzióban a részecskék diffúzióval fokozatosan képeznek egy 1.70-es dimenziós aggregátumot.
${\ displaystyle \ log _ {3} (9 * 0 {,} 75)}$	1.7381	Fraktál perkoláció 75% -os valószínűséggel	A fraktál perkolációs modell úgy épül fel, hogy minden négyzetet fokozatosan 3x3 rácsra cserélünk, amelybe egy véletlenszerű résznégyzetgyűjtemény kerül, mindegyik résznégyzetnek megmarad a p valószínűsége . A "szinte biztos" Hausdorff-dimenzió egyenlő . ${\ displaystyle \ log _ {3} (9p)}$
7/4	1.75	Kétdimenziós perkolációs klaszter határa	A percolációs klaszter határa szimulálható egy olyan lépéssel is, amely kifejezetten létrehozza a határt, vagy felhasználja a Schramm-Loewner (in) evolúciót .
${\ displaystyle {\ frac {91} {48}}}$	1.8958	Heap perkolációs két dimenzióban	A perkolációs küszöb alatt (59,3%) az inváziós perkolációs klaszter a 91/48 fraktál méretű felületet takarja. A küszöbön túl a fürt végtelen, és a 91/48 válik a "tisztások" fraktáldimenziójává.
${\ displaystyle {\ frac {\ log 2} {\ log {\ sqrt {2}}}}}$	2	Brown-mozgalom	Véletlen járás mintájára. A Hausdorff dimenzió 2-vel egyenlő marad minden dimenzióban, amely nagyobb vagy egyenlő 2-vel.
Mért	Körülbelül 2	A galaxishalmazok eloszlása	A Sloan Digital Sky Survey 2005-ös eredményeitől mérve. Lásd a hivatkozást
${\ displaystyle \ log _ {3} (13)}$	2.33	Karfiol felület	Minden ágnak körülbelül 13 ága van 3-szor rövidebb.
	2,4 ± 0,2	Összegyűrt papírgolyó	Az összegyűrt papírgömb átmérője 2 és 3 közötti nem egész teljesítményre emelve megközelítőleg arányos a felhasznált papír területével. A hajtások minden méretben kialakulnak.
	2.50	Háromdimenziós diffúziós aggregátum	Három dimenzióban a részecskék diffúzióval fokozatosan képeznek egy 2,5 dimenziós aggregátumot.
	2.50	Lichtenberg alakja	Az arboreszcens elektromos kisülések, az úgynevezett Lichtenberg-adatok, az aggregációval történő diffúzió módján nőnek.
${\ displaystyle 3 - {\ frac {1} {2}}}$	2.5	Brown- felület	Egy függvény , adja a magasságban egy pont olyan, hogy két pozitív lépésekben , és , a következőképpen egy középre Gauss-féle eloszlás variancia = . Általánosítás: A törésmutató Brown-felület ugyanazt a meghatározást követi, de varianciával = , ebben az esetben Hausdorff-dimenziója = . ${\ displaystyle f: \ mathbb {R} ^ {2} \ to \ mathbb {R}}$ $(x, y)$ $h$ $k$ ${\ displaystyle f (x + h, y + k) -f (x, y)}$ ${\ displaystyle {\ sqrt {h ^ {2} + k ^ {2}}}}$ $\ alfa$ ${\ displaystyle (h ^ {2} + k ^ {2}) ^ {\ alpha}}$ $3- \ alfa$
Mért	2.52	Heap átszivárgás 3D	A perkolációs küszöbnél a 3D inváziós percolációs klaszter fraktál dimenziója körülbelül 2,52.
Mért	2.66	Brokkoli
	2.79	Az emberi agy felülete
	2,88 - 2,97	Lung felület	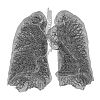A pulmonalis alveolus hálózat 3 közelében lévő fraktál felületet képez
Számított	3	Kvantum húr	A kvantum húr pályája, amelynek reprezentatív pontja véletlenszerűen származik.

Megjegyzések és hivatkozások

Falconer 2003 , p. xxv.
(a) C. Wayne Patty, alapjai Topológia , Jones & Bartlett tanulás,2009( online olvasható ) , p. 225.
(en) A DOI Feigenbaum attraktor metrikus tulajdonságairól : 10.1007 / BF01007519 .
(in) A szórás általánosított Cantor fraktálokból, arXiv : 0911.2497 .
(in) KY Tsang " Az analitikusan meghatározott furcsa vonzerők méretei " , Phys. Fordulat. Lett. , vol. 57,1986, P. 1390-1393 ( online olvasás ).
Hunt , Idézi (ban): BB Mandelbrot , Gauss-ön-affinitás és fraktálok: Globalitás, A Föld, 1 / f zaj, és R / S , Springer,2002, 654 p. ( ISBN 978-0-387-98993-8 , online olvasás ) , p. ? .
(en) " Hausdorff dimenzió és konform dinamika III: A dimenzió kiszámítása " .
A. Messaoudi, „Rauzy Fractal Frontier and Complex Number System”, Acta Arithmetica , vol. 95, n o 3, 2000, p. 195-223 [ online olvasás ] .
(en) A Fibonacci szó fraktál .
A repülőgép 2 hüllőjén, Ngai, 1999
Beryl: Eredeti fraktál .
(in) " Kör inverziós fraktálok - a határkészletek méretei " .
(in) " A sárkány határgörbéjének fraktálszerkezetéről " .
(en) Stephen Wolfram, " A binomiális együtthatók geometriája " ,1984.
(in) " Fraktáldimenzió becslése " ,1990.
(in) " " Majomfa "Fraktálgörbe " .
(in) P. Ramachandrarao, A. és D. Sinha Sanyal, " A fraktál Penrose csempézésének természetéről " [PDF] .
A Mandelbrot-készlet és a Julia-halmaz határának Hausdorff-dimenziója, arXiv : math / 9201282 .
„ Lebesgue görbe ” , a matematikai görbén (2D és 3D változatok).
Matematikáról gondolkodva , Éditions du Seuil, 1982 ( ISBN 2020060612 ) .
(en) Paul Bourke, „ Platonikus szilárd fraktálok és azok kiegészítői ” .
J. Vedikunnel, „ The Strange attraktorok ” .
(in) A Rossler-vonzó .
(in) Mark J. McGuinness, "Az fraktáldimenziója Lorenz attraktor" Physics Letters , Vol. 99A, 1983, p. 5-9. DOI : 10.1016 / 0375-9601 (83) 90052-X absztrakt .
(in) M. Borkovec, W. és R. Peikert Paris, " Az apollóniai szféra csomagolásának fraktál dimenziója " [ archívum2016. május 6] [PDF] ,1994.
[1]
(a) " Mandelbulb Hausdorff dimenziója " a fractalforums.com oldalon .
(in) Peter Mörters Yuval Peres Oded Schramm, Brown-mozgás , Cambridge University Press , 2010.
(in) " Az emberi 22. kromoszóma fraktál dimenziója " (IAFA 2003).
(in) B. Mandelbrot: " Meddig van Nagy-Britannia partja? (en) Statisztikai önhasonlóság és frakcionális dimenzió ” , Science , vol. 156, n o 37751967, P. 636-638 ( DOI 10.1126 / science.156.3775.636 , online olvasás ).
(a) Gregory F. Lawler és Oded Schramm Wendelin Werner, " A méret a Planar Brown Frontier 4/3 "2000( arXiv math / 0010165v2 ) .
Sapoval 2001 .
(a) J. Feder Fractals , Plenum Press, New York, 1988.
(a) Robert M. Ziff, " Hull-generáló séták " 1989 DOI : 10.1016 / 0167-2789 (89) 90222-4 .
(in) Muhammad Sahimi, A percolációs elmélet alkalmazásai , Taylor és Francis, 1994.
(in) "A galaxiscsoportosítás alapvető tulajdonságai a Sloan Digital Sky Survey legfrissebb eredményeinek fényében", arXiv : astro-ph / 0501583v2 .
(it) A. Filipponi, Introduzione alla fisica ,2005, 304 p. ( ISBN 978-88-08-07073-9 ).
(in) Glenn Elert, " fraktáldimenziója brokkoli " , a The Physics Factbook .
(De) Frank Grünberg, " Der Vater des Apfelmännchens " , Technológiai Szemle ,2004.
(in) K. és M. Lamrini Uahabi Atounti, " Új megközelítés a tüdő fraktál dimenziójának kiszámításához - 2015 "
(in) S. Ansoldi, " A kvantumsor Haushaus- dimenziója " a trieszti egyetemen .

Lásd is

Bibliográfia

(en) Michael F. Barnsley, Fractals Everywhere , Morgan Kaufmann ( ISBN 0120790610 )
en) Kenneth Falconer (en) , Fraktálgeometria: matematikai alapok és alkalmazások , John Wiley & Sons ,2003( 1 st szerk. 1990) ( ISBN 978-0-470-84862-3 ).
(en) Benoît Mandelbrot, A természet fraktálgeometriája, WH Freeman & Co,1982, 468 p. ( ISBN 978-0-7167-1186-5 )
(en) Heinz-Otto Peitgen (en) , A fraktál képek tudománya , Dietmar Saupe (szerkesztő), Springer Verlag (1988. augusztus), ( ISBN 0387966080 )
Bernard Sapoval, Universalités et fractales, Párizs, Flammarion , coll. "Mezők",2001( ISBN 2-08-081466-4 )